Арифметические действия над сходящимися последовательностями
Теорема. Пусть  и
и 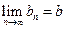 . Тогда последовательность
. Тогда последовательность 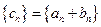 также будет сходящейся, причем
также будет сходящейся, причем 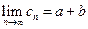 .
.
Доказательство. ►Из условия теоремы вытекает, что 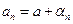 , а
, а 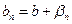
 , где
, где  и
и  - бесконечно малые последовательности. Поэтому
- бесконечно малые последовательности. Поэтому
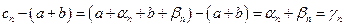 ,
,
причем 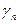 - бесконечно малая последовательность (как сумма бесконечно малых).◄
- бесконечно малая последовательность (как сумма бесконечно малых).◄
Теорема. Пусть  и
и 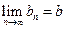 . Тогда последовательность
. Тогда последовательность 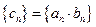 также будет сходящейся, причем
также будет сходящейся, причем 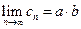 .
.
Доказательство. ►Из условия теоремы вытекает, что 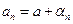 , а
, а 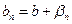
 , где
, где  и
и  - бесконечно малые последовательности. Поэтому
- бесконечно малые последовательности. Поэтому
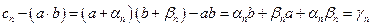 .
.
Последовательности 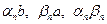 бесконечно малые как произведение бесконечно малой на ограниченную и произведение бесконечно малых последовательностей. Тогда
бесконечно малые как произведение бесконечно малой на ограниченную и произведение бесконечно малых последовательностей. Тогда  бесконечно малая как сумма бесконечно малых..◄
бесконечно малая как сумма бесконечно малых..◄
Для доказательства теоремы о пределе частного нам понадобится следующее свойство сходящихся последовательностей.
Лемма. Пусть 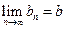 , причем
, причем 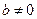 . Тогда последовательность
. Тогда последовательность 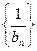 ограничена.
ограничена.
Доказательство. ►Возьмем  и найдем номер
и найдем номер  , после которого
, после которого 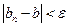 . Для всех номеров
. Для всех номеров 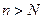 будет справедлива оценка
будет справедлива оценка
 ,
, 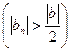 ,
,
а значит, для этих номеров 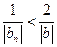 . Тогда для всех номеров
. Тогда для всех номеров  будет справедливо
будет справедливо
 ,
,
что означает ограниченность последовательности 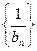 .◄
.◄
Теорема. Пусть  и
и 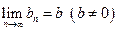 . Тогда последовательность
. Тогда последовательность 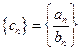 также будет сходящейся, причем
также будет сходящейся, причем  .
.
Доказательство. ►Из условия теоремы вытекает, что 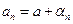 , а
, а 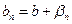
 , где
, где  и
и  - бесконечно малые последовательности. Поэтому
- бесконечно малые последовательности. Поэтому
 .
.
Последовательность  , очевидно, бесконечно малая, а, следовательно,
, очевидно, бесконечно малая, а, следовательно,  .◄
.◄
Пример. 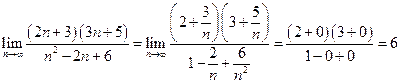 .
.