Переход к пределу в неравенствах
Теорема (о предельном переходе в неравенстве). Пусть  и
и 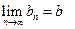 , и пусть
, и пусть 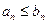 , по крайней мере, начиная с некоторого номера
, по крайней мере, начиная с некоторого номера  . Тогда
. Тогда 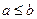 .
.
Доказательство. ►Рассмотрим последовательность 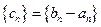 . Эта последовательность сходящаяся
. Эта последовательность сходящаяся  , кроме того,
, кроме того,  при
при  . Покажем, что
. Покажем, что  .
.
Возьмем  и выберем номер
и выберем номер  такой, что при
такой, что при 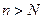
 , то есть
, то есть 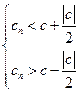 .
.
Но в таком случае, при 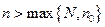 будет (мы используем только верхнее неравенство)
будет (мы используем только верхнее неравенство) 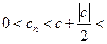 . Так как знак
. Так как знак 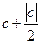 совпадает со знаком
совпадает со знаком 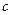 , это означает, что
, это означает, что  .◄
.◄
Теорема (о предельном переходе в двух неравенствах). Пусть  и
и 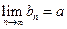 , и пусть
, и пусть  , по крайней мере, начиная с некоторого номера
, по крайней мере, начиная с некоторого номера  .
.
Тогда последовательность 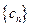 сходится и
сходится и  .
.
Доказательство. ►Фиксируем произвольное 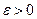 . По условию теоремы, после некоторого номера
. По условию теоремы, после некоторого номера 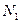 , элементы последовательности
, элементы последовательности  будут находиться в
будут находиться в  , а, после номера
, а, после номера 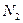 , в той же окрестности будут находиться все члены последовательности
, в той же окрестности будут находиться все члены последовательности 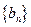 . Тогда для номеров
. Тогда для номеров 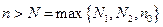 элемент последовательности
элемент последовательности 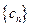 , находясь между
, находясь между 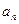 и
и 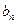 , тоже попадет в
, тоже попадет в  .◄
.◄
Пример.  , если
, если 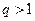 .
.
Доказательство.► Запишем  как
как 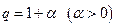 . Воспользуемся формулой бинома Ньютона
. Воспользуемся формулой бинома Ньютона
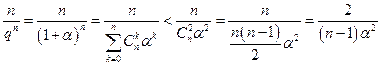 .
.
То есть

а так как 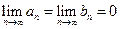 , то и
, то и  .◄
.◄
Следствие. 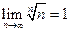 .
.
Доказательство. ►Фиксируем произвольное 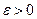 . С учетом предыдущего примера имеем
. С учетом предыдущего примера имеем  . Тогда найдется такой номер
. Тогда найдется такой номер  , что для всех
, что для всех 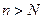 будет
будет  . Кроме того, очевидно,
. Кроме того, очевидно, 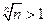 . То есть для всех
. То есть для всех 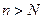 получим
получим  .◄
.◄
Задача. Доказать, что 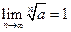 .
.
Доказательство. ►Пусть 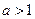 . Очевидно, что
. Очевидно, что 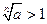 , а, начиная с некоторого номера
, а, начиная с некоторого номера  . Далее воспользуемся результатом предыдущего примера и теоремой о переходе к пределу в двух неравенствах.
. Далее воспользуемся результатом предыдущего примера и теоремой о переходе к пределу в двух неравенствах.
Если  , то
, то  . Поэтому в последнем примере требуется только условие
. Поэтому в последнем примере требуется только условие  .◄
.◄