Односторонние пределы и односторонняя непрерывность
Определение. Пусть функция 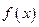 определена в левой полуокрестности точки
определена в левой полуокрестности точки  . Говорят, что она имеет предел
. Говорят, что она имеет предел  при
при 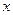 , стремящемся к
, стремящемся к  слева и пишут
слева и пишут
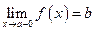 или
или 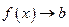
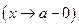
если для любого 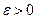 существует такое
существует такое 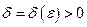 , что
, что 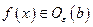 при
при 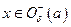 .
.
Записанное с неравенствами это определение выглядит следующим образом:
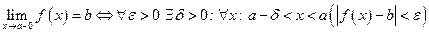 .
.
Пример. 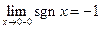 (
(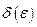 - произвольно).
- произвольно).
Упражнение. По аналогии с предыдущим запишите определение 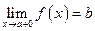 , приведите пример.
, приведите пример.
Для конечных односторонних пределов в точке  используются обозначения
используются обозначения 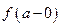 (предел слева) и
(предел слева) и 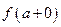 (предел справа).
(предел справа).
Упражнение. Дайте определение односторонних пределов:
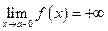 ,
, 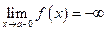 ,
, 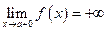 ,
, 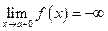 ,
,
приведите примеры.
Утверждение. Функция 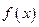 имеет предел
имеет предел  при
при 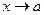 тогда и только тогда, когда существуют и равны
тогда и только тогда, когда существуют и равны  оба односторонние предела:
оба односторонние предела:
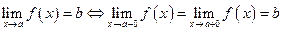 .
.
Доказательство. 4 Пусть 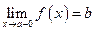 , тогда
, тогда
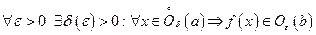 (1)
(1)
Так как 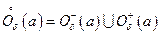 , то из (1) вытекает
, то из (1) вытекает
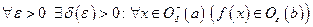 ,
,
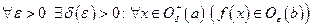 ,
,
то есть
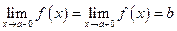 .
.
Пусть теперь существуют и равны  оба односторонних предела. Фиксируем произвольное
оба односторонних предела. Фиксируем произвольное 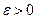 . Из существования односторонних пределов следует, что
. Из существования односторонних пределов следует, что
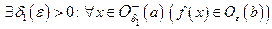 ,
,
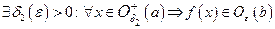 .
.
Возьмем 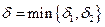 . Очевидно, что
. Очевидно, что 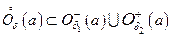 . Но тогда из
. Но тогда из 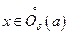 будет следовать
будет следовать 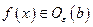 .3
.3
Пример. Функция
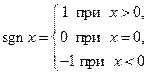
(от латинского signum - знак) определена на всей числовой оси. Покажем, что у нее нет предела при 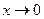 .
.
Доказательство. 4Очевидно, что 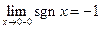 , а
, а 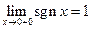 , то есть левый и правый пределы не равны, то есть
, то есть левый и правый пределы не равны, то есть 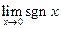 не существует. 3
не существует. 3
Определение. Пусть функция 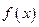 определена на некотором полуинтервале
определена на некотором полуинтервале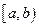 . Она называется непрерывной в точке
. Она называется непрерывной в точке  справа, если
справа, если
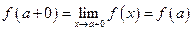 .
.
Запишем это определение в терминах окрестностей
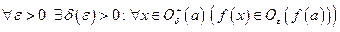 ,
,
и в терминах неравенств
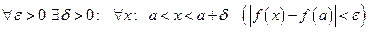 .
.
Аналогично определяется непрерывность в точке  слева.
слева.
Упражнение. Сформулируйте это определение.
Упражнение. Докажите, что функция 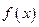 непрерывна в точке
непрерывна в точке  тогда и только тогда, когда она непрерывна в
тогда и только тогда, когда она непрерывна в  слева и справа.
слева и справа.
Определение. Функция 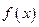 называется непрерывной на отрезке
называется непрерывной на отрезке 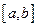 , если она непрерывна на интервале
, если она непрерывна на интервале 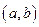 , а также непрерывна в точке
, а также непрерывна в точке  справа, а в точке
справа, а в точке  слева.
слева.