Определение предела и непрерывности по Гейне
Между понятием предела последовательности и понятием предела функции имеется тесная связь.
Теорема. Функция 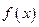 имеет предел
имеет предел  при
при 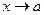 тогда и только тогда, когда
тогда и только тогда, когда  для любой последовательности
для любой последовательности 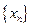 такой, что
такой, что 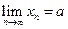 и
и  .
.
Доказательство. 4Пусть 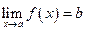 и
и 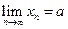 ,
, 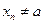 . Тогда
. Тогда
 . (1)
. (1)
Из сходимости же последовательности 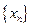 к
к  следует существование такого номера
следует существование такого номера  , что для всех
, что для всех 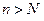 будет
будет 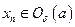 , а так как
, а так как 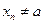 , то
, то
 . (2)
. (2)
Объединяя (1) и (2), получим
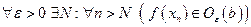 ,
,
то есть
 .
.
Пусть теперь  для любой последовательности
для любой последовательности 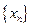 , сходящейся к
, сходящейся к  и такой, что
и такой, что 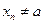 . Если
. Если  не является пределом
не является пределом 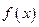 при
при 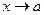 , то найдется окрестность
, то найдется окрестность 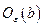 такая, что при любом
такая, что при любом 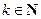 найдется точка
найдется точка 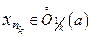 такая, что
такая, что  . Но это означает, что подпоследовательность
. Но это означает, что подпоследовательность 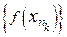 не сходится к
не сходится к  , хотя последовательность
, хотя последовательность 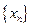 стремится к
стремится к  .3
.3
Из доказанной теоремы следует, что данное ранее определение предела (по Коши) эквивалентно следующему определению (по Гейне):
Определение. Говорят, что функция 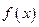 имеет предел
имеет предел  при
при 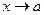 , если
, если  для любой последовательности
для любой последовательности 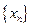 такой, что
такой, что 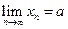 и
и  .
.
Дадим также определение непрерывности по Гейне. Здесь можно отказаться от условия 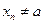 .
.
Определение. Функция  непрерывна в точке
непрерывна в точке  , если
, если 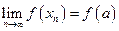 для любой последовательности
для любой последовательности 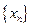 такой, что
такой, что 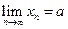
Так же, как и в случае предела функции, определения непрерывности по Коши и по Гейне эквивалентны.
Упражнение. Докажите это утверждение.