Частные производные функции нескольких переменных.
Опять остановимся на случае действительнозначной функции двух переменных.
Определение. Частным приращением  функции
функции 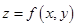 в точке
в точке  , соответствующим приращению
, соответствующим приращению  переменной
переменной  называется величина
называется величина
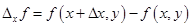 .
.
Аналогично определяется частное приращение
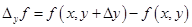 .
.
Определение. Частной производной функции 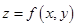 по переменной
по переменной 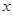 в точке
в точке  называется предел (если он существует)
называется предел (если он существует)
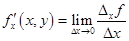 .
.
Аналогично определяется частная производная по переменной 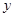 :
:
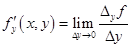 .
.
Связь между непрерывностью, дифференцируемостью функции и существованием ее частных производных.
Теорема. Если функция 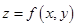 дифференцируема в точке
дифференцируема в точке  , то у нее существуют обе частные производные
, то у нее существуют обе частные производные 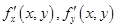 , причем
, причем
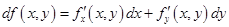 .
.
Доказательство.  Так как функция
Так как функция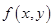 дифференцируема в точке
дифференцируема в точке  , то
, то
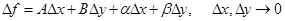 ,
,
а если 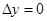 , то
, то
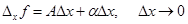 ,
,
поэтому
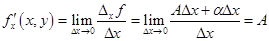 .
.
Аналогично получаем
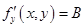 .
.
Из существования частных производных непрерывность и дифференцируемость функции, вообще говоря, не вытекает, что мы продемонстрируем на следующем примере.
Пример. Рассмотрим функцию двух переменных
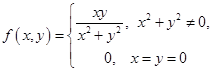 .
.
Эта функция, как нам известно, разрывна в нуле, а, следовательно, и не дифференцируема в нем. Тем не менее, имеем
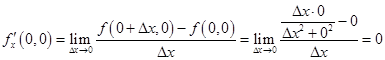 .
.
Аналогично можно показать, что 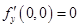 .
.
Справедлива, однако, следующая теорема.
Теорема. Пусть функция 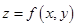 непрерывна вместе со своими частными производными
непрерывна вместе со своими частными производными  в окрестности точки
в окрестности точки 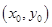 . Тогда она будет дифференцируема в этой точке.
. Тогда она будет дифференцируема в этой точке.
Доказательство.  Представим полное приращение функции
Представим полное приращение функции 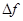 в виде
в виде
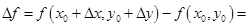
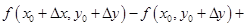
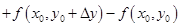 .
.
Каждая из этих разностей представляет частное приращение функции лишь по одной переменной. Применяя к каждой из этих разностей формулу конечных приращений, получим
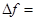
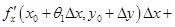
 .
.
Из непрерывности частных производных в окрестности точки 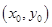 следует, что
следует, что
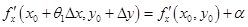 ,
,
 ,
,
где  - бесконечно малые функции при
- бесконечно малые функции при 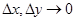 . Используя полученные выражения, получим
. Используя полученные выражения, получим
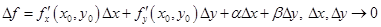 .
.