Производная от сложной функции.
Пусть в открытой области 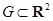 задана функция
задана функция 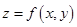 , непрерывная вместе со своими частными производными
, непрерывная вместе со своими частными производными 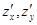 в
в 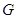 , и пусть переменные
, и пусть переменные  являются непрерывно дифференцируемыми функциями от переменной
являются непрерывно дифференцируемыми функциями от переменной  на промежутке
на промежутке 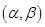
 , причем при
, причем при 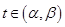 точка
точка  . Тогда мы можем рассмотреть сложную функцию
. Тогда мы можем рассмотреть сложную функцию  , определенную на
, определенную на 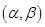 .
.
Покажем, что эта функция дифференцируема, и вычислим ее производную. Итак, фиксируем точку  . Придадим переменной
. Придадим переменной  некоторое приращение
некоторое приращение 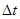 , ему будут соответствовать приращения
, ему будут соответствовать приращения 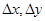 переменных
переменных  . Поскольку частные производные функции
. Поскольку частные производные функции 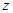 непрерывны в окрестности этой точки, она дифференцируема в
непрерывны в окрестности этой точки, она дифференцируема в  и соответствующее ее приращение представимо в виде
и соответствующее ее приращение представимо в виде
 ,
,
где 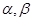 - бесконечно малые функции при
- бесконечно малые функции при  .
.
Разделив обе части последнего равенства на 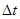 , получим
, получим
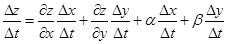 .
.
Так как  непрерывны, то при
непрерывны, то при  будет
будет 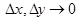 и, соответственно,
и, соответственно, 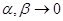 . Воспользовавшись также существованием производных
. Воспользовавшись также существованием производных  , в пределе получим
, в пределе получим
 .
.
Теперь рассмотрим случай, когда  зависят от нескольких переменных, например, от двух:
зависят от нескольких переменных, например, от двух: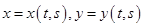 (случай большего количества переменным ничем принципиально от этого не отличается). Будем предполагать по аналогии с одномерным случаем, что
(случай большего количества переменным ничем принципиально от этого не отличается). Будем предполагать по аналогии с одномерным случаем, что  имеют непрерывные частные производные по переменным
имеют непрерывные частные производные по переменным  и
и 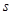 .
.
Вопрос существования частных производных 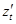 и
и 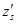 существенно не отличается от рассмотренного ранее, поскольку при вычислении частной производной одну из двух переменных мы фиксируем, и у нас остается функция, зависящая только от одной переменной. Для этого случая получим
существенно не отличается от рассмотренного ранее, поскольку при вычислении частной производной одну из двух переменных мы фиксируем, и у нас остается функция, зависящая только от одной переменной. Для этого случая получим
 ,
,
аналогичная формула получается для производной по переменной 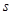 .
.