Интеграл с переменным верхним пределом
Пусть функция  интегрируема на отрезке
интегрируема на отрезке 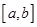 . Определим на этом же отрезке функцию
. Определим на этом же отрезке функцию
 ,
,
которую часто называют интегралом с переменным верхним пределом. Из свойства аддитивности определенного интеграла вытекает корректность определения функции 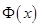 для
для 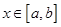 .
.
Теорема (о непрерывности интеграла с переменным верхним пределом). Если функция  интегрируема на отрезке
интегрируема на отрезке 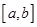 , то функция
, то функция  будет непрерывной на этом отрезке.
будет непрерывной на этом отрезке.
Доказательство. 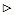 Интегрируемая на отрезке функция ограничена на нем, то есть существует такое число
Интегрируемая на отрезке функция ограничена на нем, то есть существует такое число 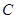 , что
, что 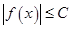 на
на 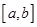 . Пусть
. Пусть 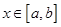 , и пусть
, и пусть  - приращение независимой переменной, при котором
- приращение независимой переменной, при котором 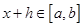 . Воспользовавшись свойством аддитивности, а также теоремами об оценках определенного интеграла, получим
. Воспользовавшись свойством аддитивности, а также теоремами об оценках определенного интеграла, получим
 .
.
То есть 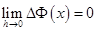 , что означает непрерывность функции
, что означает непрерывность функции 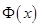 в точке
в точке 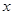 .
.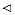
Теорема (о дифференцируемости интеграла с переменным верхним пределом). Пусть функция  непрерывна на отрезке
непрерывна на отрезке 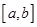 . Тогда функция
. Тогда функция  будет дифференцируемой на этом отрезке.
будет дифференцируемой на этом отрезке.
Доказательство.
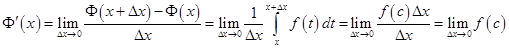 ,
,
где 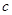 лежит между
лежит между 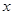 и
и 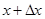 . Из непрерывности
. Из непрерывности  следует, что при
следует, что при 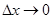 будет справедливо
будет справедливо 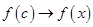 .
.