Площадь криволинейной трапеции.
Пусть  - неотрицательная интегрируемая функция, заданная на отрезке
- неотрицательная интегрируемая функция, заданная на отрезке  . Рассмотрим криволинейную трапецию
. Рассмотрим криволинейную трапецию  , определенную неравенствами:
, определенную неравенствами: 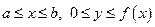 . Верхние суммы Дарбу для
. Верхние суммы Дарбу для  являются площадями многоугольников, содержащих
являются площадями многоугольников, содержащих  , а, соответственно, нижние – площадями многоугольников, целиком содержащихся в
, а, соответственно, нижние – площадями многоугольников, целиком содержащихся в  . Таким образом, получаем
. Таким образом, получаем
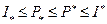 . Из интегрируемости
. Из интегрируемости  на отрезке
на отрезке  следует, что
следует, что 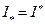 , а, значит, фигура
, а, значит, фигура  квадрируема и
квадрируема и
 .
.
Если функция отрицательна, то интеграл равен площади, взятой со знаком минус, если же меняет знак, то равен алгебраической сумме площадей.
Если криволинейная трапеция снизу и сверху ограничена кривыми
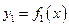 и
и 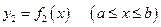 ,
,
то площадь такой трапеции будет равна
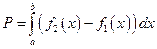 .
.
Пример 4. Найти площадь области, ограниченной кривыми 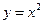 и
и 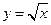 .
.
Решение:  .
.