Площадь фигуры, заданной в полярных координатах.
Найдем площадь сектора  , ограниченного непрерывной кривой
, ограниченного непрерывной кривой  и двумя полупрямыми
и двумя полупрямыми  и
и 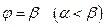 . Рассмотрим разбиение отрезка
. Рассмотрим разбиение отрезка 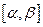 -
- 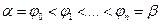 и проведем соответствующие этим углам радиус-векторы. Пусть
и проведем соответствующие этим углам радиус-векторы. Пусть 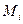 и
и 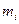 соответственно наибольшее и наименьшее значение функции
соответственно наибольшее и наименьшее значение функции 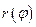 в промежутке
в промежутке 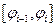 . Площадь множества круговых секторов, ограниченных радиус-векторами
. Площадь множества круговых секторов, ограниченных радиус-векторами  и целиком содержащихся в
и целиком содержащихся в , равна
, равна 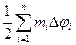 , площадь круговых секторов с теми же самыми радиус-векторами, содержащих
, площадь круговых секторов с теми же самыми радиус-векторами, содержащих  , равна
, равна 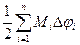 . Эти числа являются соответственно нижней и верхней суммами Дарбу для интеграла
. Эти числа являются соответственно нижней и верхней суммами Дарбу для интеграла 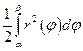 и имеют пределом этот интеграл. Получаем
и имеют пределом этот интеграл. Получаем
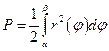 .
.
Пример 5. Найти площадь сектора, ограниченного окружностью  и лучами
и лучами  и
и 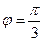 .
.
Решение: 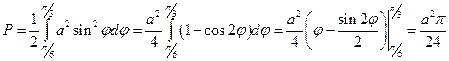 .
.
Объем тела вращения.
Выведем формулу для вычисления объема тела  , полученного при вращении кривой
, полученного при вращении кривой 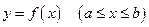 вокруг оси
вокруг оси  . Для этого разобьем
. Для этого разобьем  на части
на части 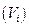 плоскостями, перпендикулярными оси
плоскостями, перпендикулярными оси  и проходящими через точки
и проходящими через точки 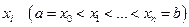 . Часть
. Часть 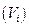 содержит в себе цилиндр, в основании которого лежит круг радиуса
содержит в себе цилиндр, в основании которого лежит круг радиуса 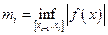 , а высота равна
, а высота равна 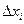 . Аналогично,
. Аналогично, 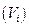 содержится в цилиндре с круговым основанием радиуса
содержится в цилиндре с круговым основанием радиуса 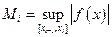 и той же высотой. Объемы полученных частей будут равны соответственно,
и той же высотой. Объемы полученных частей будут равны соответственно, 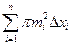 и
и  , то есть совпадают с нижней и верхней суммами Дарбу для интеграла
, то есть совпадают с нижней и верхней суммами Дарбу для интеграла  . Окончательно получаем
. Окончательно получаем
 .
.
Пример 6. Найти объем шара радиуса  .
.
Решение: 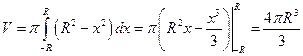 .
.