СЛОЖЕНИЕ МОМЕНТОВ

 

Пусть система состоит из двух частей, которым соответствуют полные моменты ⁽¹⁾ и ⁽²⁾. Так как эти операторы действуют только на свои переменные, то они взаимно коммутируют:

 

[⁽¹⁾, ⁽²⁾] = ,

 

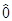причем, между собой операторы каждой группы коммутируют обычным способом:

[_j^(a),_k^(a)] = ie_{jkl l}^(a), [^(a)2,_j^(a)] = .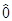

 

У полной системы имеются состояния с определенными значениями квадратов моментов 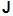⁽¹⁾² и 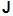⁽²⁾² и их проекций на третью ось 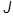₃⁽¹⁾ и 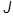₃⁽²⁾:

 

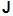⁽¹⁾² = ²j₁(j₁+1), 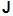⁽²⁾² = ²j₂(j₂+1), 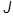₃⁽¹⁾ = m₁, J₃⁽²⁾ = m₂.

 

Эти состояния описываются векторами

 

|j₁m₁j₂m₂ñ = |j₁m₁ñ|j₂m₂ñ,

 

являющимися собственными для каждого из операторов ⁽¹⁾², ⁽²⁾²,₃⁽¹⁾ и ₃⁽²⁾ с указанными собственными значениями. Эти векторы образуют базис в пространстве состояний полной системы, и по нему можно разложить произвольный вектор ее состояния:

 

|yñ =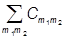|j₁m₁j₂m₂ñ, C_m1C_m2 = áj₁m₁j₂m₂|yñ.

 

Введем оператор полного момента

 

=⁽¹⁾+⁽²⁾.

­­­­­­

Для него справедливы обычные коммутационные соотношения

 

[_j,_k] = ie_{jkl l}, [²,_j] = .

 

Каждый из введенных базисных векторов будет собственным для оператора

₃ = ₃⁽¹⁾ +₃⁽²⁾

 

с собственным значением

 

J₃ = (m₁+m₂) º m.

 

Действительно,

 

₃|j₁m₁j₂m₂ñ =₃⁽¹⁾|j₁m₁j₂m₂ñ +₃⁽²⁾|j₁m₁j₂m₂ñ = m₁|j₁m₁j₂m₂ñ + m₂|j₁m₁j₂m₂ñ.

Оператор квадрата полного момента

 

² = ⁽¹⁾² + ⁽²⁾² + 2^{(1) (2)}

 

коммутирует с операторами ⁽¹⁾² и ⁽²⁾², а потому он может иметь определенное значение J²вместе с квадратами моментов каждой из подсистем. Однако, старые векторы не будут собственными для этого оператора из-за наличия в нем третьего слагаемого, которое будет перемешивать состояния с разными m.

Но можно всегда построить новый базис из векторов

|j₁j₂jmñ,

 

которые являются собственными для ² и ₃:

 

²|j₁j₂jmñ = ²j(j +1) |j₁j₂jmñ, 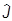₃|j₁j₂jmñ = m|j₁j₂jmñ,

 

т.е. описывают состояния с определенными j₁,j₂ (это всегда), а также с определенными j и m. Как уже говорилось, любые векторы, а значит и эти, можно разложить по старому базису:

 

|j₁j₂jmñ =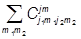|j₁m₁j₂m₂ñ, 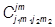áj₁m₁j₂m₂|j₁j₂jmñ.

 

Возникающие здесь важные числа C^..._...называются коэффициентами Клебша-Гордона, причем фазовые множители у новых базисных векторов всегда можно выбрать так, чтобы эти коэффициенты были вещественными. Для них имеются общие формулы, но они очень сложны. Поэтому существуют специальные таблицы коэффициентов Клебша-Гордона (ККГ).

ККГ задают матрицу преобразования от представления, в котором заданы проекции моментов подсистем (и их моменты) к представлению, в котором задан полный момент и его проекция (и моменты подсистем). Эта матрица осуществляет переход от одного ортонормированного базиса к другому, а потому она унитарна:

 

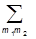áj₁m₁j₂m₂|jmñáj₁m₁j₂m₂|jm^¢ñ = d_jj¢d_mm¢

или

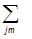áj₁m₁j₂m₂|jmñáj₁m₁^¢j₂m₂^¢|jmñ = d_m1m¢1d_m2m¢2.

 

Обратный переход осуществляется обратной матрицей, которая в силу унитарности, равна эрмитово сопряженной матрице, а в силу вещественности - просто транспонированной к исходной матрице:

|j₁m₁j₂m₂ñ = 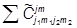|j₁j₂jmñ,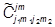= áj₁j₂jm|j₁m₁j₂m₂ñ.

 

Мы уже установили, что каждый старый вектор |j₁m₁j₂m₂ñ является собственным для оператора ₃ с собственным значением

J₃ = (m₁+m₂).

Поэтому

m = m₁+m₂

 

и суммирование в разложении ККГ по одному из индексов носит формальный характер. Так как m₂=m-m₁, то при заданном m суммирование можно вести только по m₁. Это отвечает тому, что

 

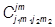~ d_m,m1+m2.

 

Важная задача - определение возможных значений j при заданных j₁ и j₂. Для ее решения исследуем возможные значения m. Его максимальное значение есть m=j₁+j₂ . Оно осуществляется в одном единственном состоянии |j₁j₁ñ|j₂j₂ñ, которое будет иметь

 

j = j₁ + j₂.

 

Следующее значение m=j₁+j₂-1 может осуществляться двумя линейными комбинациями векторов

 

|j_1,j₁-1ñ|j_2,j₂ñ и |j_1,j₁ñ|j_2,j₂-1ñ.

 

Одна из них отвечает уже найденному моменту j=j₁+j₂ ( вектор торчит несколько «вбок»), а другая - значению

 

j = j₁ + j₂ - 1

 

(вектор направлен по оси). Значению m=j₁+j₂-2 будут отвечать три линейные комбинации из трех векторов

|j_1,j₁-2ñ|j₂j₂ñ, |j_1,j₁-1ñ|j_2,j₂-1ñ, |j_1,j₁ñ|j_2,j₂-2ñ.

 

Одна отвечает значению j=j₁+j₂ (еще больше вбок), другая - значению j=j₁+j₂-1 (немножко вбок) и третья - значению

 

j = j₁ + j₂ - 2

 

(вдоль оси). Продолжая процесс, убедимся, что на каждом этапе, когда m уменьшается на 1, появляется новое значение j до тех пор, пока не дойдем до значений, при которых либо m₁=-j₁, либо m₂ =-j₂. Таким образом, минимальное значение есть

j = (j₁ - j₂).

 

Итак, получаем следующее правило сложения моментов импульса: при заданных значениях j₁ и j₂ квантовое число j может пробегать множество значений через 1 из интервала

|j₁-j₂| £ j £ j₁ + j₂.

 

Каждому j отвечает 2j+1 состояний, а потому всего их будет

= (2j₁ + 1)(2j₂ + 1)

(сумма арифметической прогрессии). Это совпадает с числом «старых» состояний |j₁m₁ñ|j₂m₂ñ, которое очевидным образом равно (2j₁+1)(2j₂+1). Конечно, так и должно быть, и совпадение подтверждает правильность найденного правила сложения моментов. Полученные неравенства допускают простую геометрическую интерпретацию - как неравенства для сторон треугольника. Поэтому их называют соотношением треугольника и кратко записывают как D(j j₁ j₂). Числа j, j₁, j₂ входят в соотношение треугольника симметрично. Если они не выполняются, то ККГ автоматически обращаются в нуль.

В качестве операторов ⁽¹⁾ и ⁽²⁾ можно рассматривать операторы орбитального момента и спинового момента 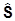- ведь важно лишь то, что разные операторы коммутируют друг с другом, а для и 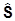это так. В частности, очень важен случай S = 1/2 (электрон). Если l ¹ 0, то полный момент j может принимать два значения:

 

l+1/2 и l-1/2.

 

Но в S- состоянии, когда l = 0 , полный момент равен 1/2, и только. Таким образом, получаем следующие возможные состояния электрона:

 

s_1/2; p_1/2; p_3/2; d_3/2; d_5/2;...

 

Всего таких состояний имеется:

 

s-2, p-2+4 = 6, d-4+6=10,...

 

Число же низших состояний таково:

 

s-2, s, p-8, s, p, d-18,...

 

Очень похоже на числа заполнения в таблице Менделеева, и недаром. Ведь в атоме при n=2 есть s- и p- состояния, откуда - 8, при n= 3 есть s-, p- и d- состояния, откуда - 18, т.д.

При сложении орбитального момента электрона с его спином полезно знать соответствующие разложения. Поэтому приведем таблицу ККГ:

 

	ms = +1/2	ms = -1/2
j = l + 1/2
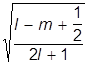
j = l – 1/2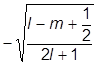

Запишем также для справок волновые функции электрона в центральном

поле, где сохраняются и :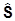

 

s = 1/2, m_s = +1/2, -1/2,

 

l, m_l = m-m_s

 

Разложение волновой функции состояния с определенными значениями энергии, орбитального момента l (спина s), полного момента j и его проекции m по состояниям с определенными значениями 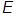, l, m_l, s, m_s имеет вид

 

y_Elsjm( r ,s)= ,

 

где - спиновая переменная, а - спиновые функции. Разложение можно записать короче:

y_Elsjm( r ,s) =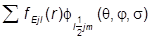

где f - сферические функции со спином (шаровые функции):

 

;

 

.
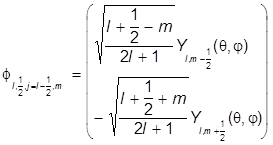