КОЭФФИЦИЕНТ ПРОХОЖДЕНИЯ
|
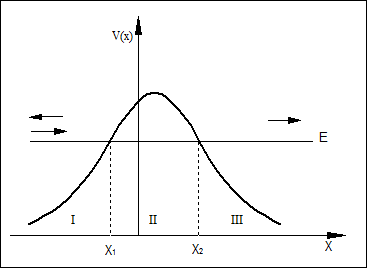
В качестве примера применения метода ВКБ вычислим коэффициент прохождения частицы через барьер произвольной формы (а не прямоугольной). При этом считаются выполненными условия квазиклассичности, т.е. барьер - достаточно плавный. Это значит, помимо всего прочего, что он широкий, и что энергия много меньше высоты барьера. Идея: задаем волновую функцию в области I в виде суперпозиции падающей и отраженной волн, «протягиваем» ее по полученному рецепту в область II, а затем по несколько модифицированному рецепту в область III и требуем, чтобы там не было отраженной волны.
I. yI(x) = 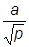 [sin (z +
[sin (z +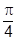 ) +
) + cos(z +
cos(z +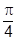 )]
)]
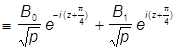 º yпад(x) + yотр(x).
º yпад(x) + yотр(x).
z = 
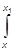 p(y)dy, B0 = 1/2(b+ia), B1 = 1/2(b-ia)
p(y)dy, B0 = 1/2(b+ia), B1 = 1/2(b-ia)
II. yII(x) = 
|z| =  |p(y)dy|,
|p(y)dy|,  ;
;

yII(x) = 


III. yIII (x) = 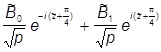 ,
,
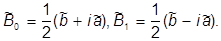
Но в области III не должно быть отраженной волны (по постановке задачи - частицы падают из -µ, частично отражаются, а частично уходят на +µ). Поэтому
 = 0 Þ
= 0 Þ 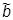 = -i
= -i ;
;
 ;
;
B0=1/2 (b+ia) = 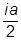 (1/4 e-2g +1)
(1/4 e-2g +1)
B1 = 1/2 (b-ia) = 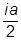 (1/4 e-2g - 1).
(1/4 e-2g - 1).
Таким образом, все коэффициенты выражаются через a, который можно (но в данной задаче не нужно) найти из условия нормировки:
b = 
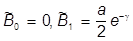 .
.
Здесь следует выделить B0 (коэффициент при падающей волне) и 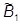 (коэффициент при отраженной волне). Вводим коэффициенты прохождения и отражения
(коэффициент при отраженной волне). Вводим коэффициенты прохождения и отражения
D = 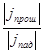 , R =
, R = 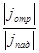 ,
,
где токи выражаются через соответствующие волновые функции:
j = 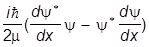 .
.
Подставляя найденные коэффициенты получим
D = 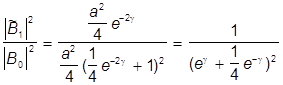 ,
,
R = 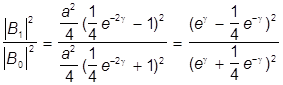
Но здесь произошло некоторое превышение точности. В частности, D+R¹1, в противоречии с сохранением вероятности (куда делись частицы?). Однако нужно учесть, что
g =  >>1.
>>1.
Тогда равенство D+R=1 , будет выполняться с точностью до слагаемых типа exp(-2g) и exp(-4g), которые тем самым нужно отбросить. Их нужно отбросить и в выражении для D, для которого окончательно получаем
D = e-2g = exp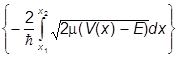 .
.
Это весьма важная формула, и она часто применяется - например, при анализе альфа-распада ядер, механизм которого, как известно, туннельный.