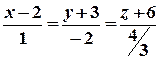Касательная плоскость и нормаль к поверхности

 

Касательной плоскостью к поверхности S в её точке М₀ называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности S через точку М₀.

Уравнение касательной плоскости к поверхности, заданной равнением z = f(x,y), в точке M₀(x₀,y₀,z₀) имеет вид:

 

z – z₀ = f’_x(x₀,y₀)(x – x₀) + f’_y(x₀,y₀)(y – y₀) (1)

Вектор 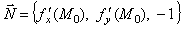называется вектором нормали к поверхности S в точке М₀. Вектор нормали перпендикулярен касательной плоскости.

Нормалью к поверхности S в точке М₀ называется прямая, проходящая через эту точку и имеющая направление вектора N. Канонические уравнения нормали к поверхности, заданной уравнением z = f(x,y), в точке M₀(x₀,y₀,z₀), где z₀ = f(x₀,y₀), имеют вид:

 

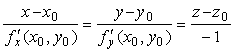(2)

Пусть поверхность 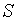задана уравнением

(3)

в неявном виде. Будем считать, что 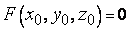и в некоторой окрестности точки 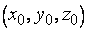функция 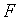имеет непрерывные частные производные, одновременно не равные нулю. Тогда

(4)

Условимся писать 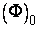вместо .

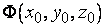Уравнение касательной плоскости к 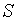в точке 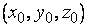запишется так:

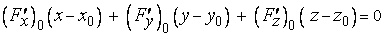, (5)

а уравнение нормали к 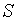в точке 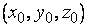- так:

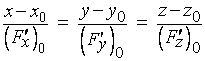. (6)

Пример 1. Уравнение

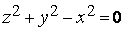(7)

определяет круговой конус с вершиной в начале координат и осью, совпадающей с осью 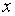(рис. 1).

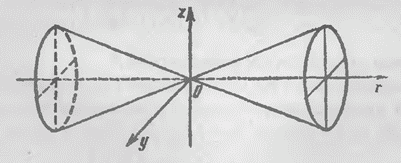
Рис. 1

Левая часть уравнения (7) имеет частные производные

,

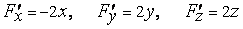одновременно не равные нулю, если точка 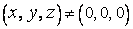. В любой такой точке, которую обозначим через 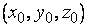, касательная плоскость определяется уравнением

.

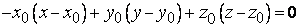Нормаль к 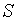в точке 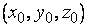, т. е. прямая, проходящая через эту точку, перепендикулярно к касательной плоскости, очевидно, имеет уравнение

.

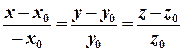Пример 2. Найти уравнение касательной плоскости и уравнение нормали к поверхности

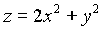в точке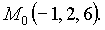

Решение: Имеем

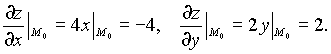
Тогда, согласно (1), уравнение касательной плоскости к данной поверхности в указанной точке будет иметь вид: z - 6 = - 4(x + 1) + 2(y - 2), то есть

4x - 2y + z + 2 = 0, а уравнение нормали, согласно (2):

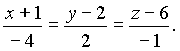
Пример 3. Найти уравнение касательной плоскости и нормали к конусу

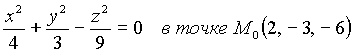
Решение. Имеем

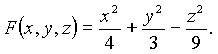
Тогда

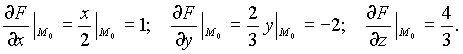
Уравнение касательной плоскости запишем в виде

или .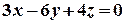

Уравнение нормали имеет вид