Теорема 2 (достаточные условия существования экстремума).

Пусть функция z = f(х, у) в критической точке М₀(х₀, у₀) и некоторой

её окрестности имеет непрерывные частные производные второго

порядка. Положим

 

.

 

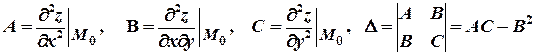Тогда:

1) если ∆ > 0, то функция z = f(х, у) имеет экстремум в точке

М₀(х₀, у₀): максимум, если А< 0 и минимум, если А > 0;

 

2) если ∆<0, то функция z=f(х, у) в точке М₀(х₀,, у₀) экстремума не имеет;

3) в случае, если ∆ = 0, то в точке М₀(х₀, у₀) экстремум может быть,

может не быть. Необходимы дополнительные исследования.

 

 

Пример 4. Исследовать на экстремум функцию z = 3xy – x²y – xy² .

 

Решение. Областью определения функции является множество точек на плоскости XОY, т.е. (х, у) Î R². Найдем частные производные функции:

; .

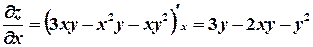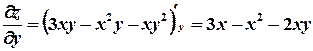Точки, в которых частные производные не существуют, отсутствуют.

Следовательно, критические точки найдем, решая систему уравнений:

 

.

 

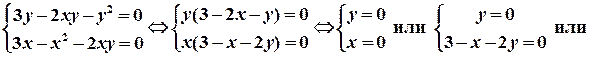
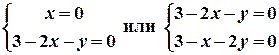Отсюда получим точки: М₁(0, 0), М₂(3, 0), М₃(0, 3), М₄(1, 1).

 

Найдем частные производные второго порядка данной функции:

 

, ,

.

 

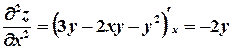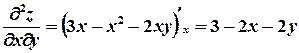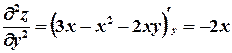В точке М₁(0, 0) имеем: А₁ = 0, В₁ = 3, С₁ = 0, ∆₁ = АС – В² = –9 < 0.

Т.к. ∆₁ < 0, то в точке М₁(0, 0) функция экстремума не имеет.

В точке М₂(3, 0) имеем: А₂ = 0, В₂ = –3, С₂ = –6, ∆₂ = –9 < 0. Также

экстремума нет.

В точке М₃(0, 3) имеем: А₃ = –6, В₂ = –3, С₃ = 0, ∆₃ = –9 < 0. Функция

экстремума не имеет.

В точке М₄(1, 1) имеем: А₄ = –2, В₄ = –1, С₄ = –2, ∆₄ = 3, т.е. ∆₄ > 0.

Т.к. А₄<0, то в точке М₄ функция имеет максимум: z_max=z(1; 1)=3 –1 – 1 =1.