Интегральная сумма. Определенный интеграл

 

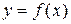Рассмотрим на отрезке непрерывную функцию , принимающую неотрицательные значения .

Выполним следующие действия:

1. С помощью точек , где 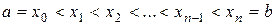, разобьем отрезок на n-частичных отрезков .

2. В каждом частичном отрезке 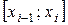выберем произвольную точку 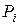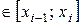и вычислим значение функции в ней, т.е. величину .

3. Умножим найденное значение функцийна длину 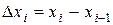соответствующего частичного отрезка: .

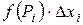4. Составим сумму 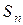всех таких произведений:

. (16)

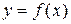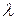Сумма вида (16) называется интегральной суммой функции на отрезке . Обозначим через длину наибольшего частичного отрезка: .

5. Найдем предел интегральной суммы (16), когда 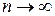, при этом .

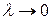Если интегральная сумма 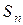имеет предел, который не зависит ни от способа разбиения отрезка на частичные отрезки, ни от выбора точек в них, то это число называется определенным интегралом.

 

Определение. Определенным интегралом от функции на отрезке

называется число, равное пределу, к которому стремится инте-

гральная сумма 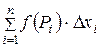при условии, что максимальная

длина частей разбиения 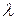стремится к нулю:

. (17)

Числа а и b называются соответственно нижним и верхнимпределами интегрирования, f(х) – подынтегральной функцией, f(x)dx – подынтегральным выражением, х – переменной интегрирования, отрезок - отрезком интегрирования.

Функция 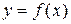, для которой на отрезке существует определенный интеграл 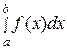, называется интегрируемой на этом отрезке.

Теорема (существования интеграла). Если функция 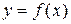непрерывна

на отрезке , то она интегрируема на этом отрезке, т.е. определенный интеграл от этой функции существует.