Несобственные интегралы с бесконечными пределами

интегрирования (I рода)

 

Пусть функция f(х) непрерывна на промежутке 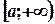. Тогда для любого отрезка 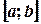интеграл существует. При изменении b интеграл изменяется, т.е. он является непрерывной функцией b. Рассмотрим поведение этого интеграла при .

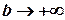Определение. Если существует конечный предел 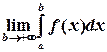, то его назы-

вают несобственным интеграломI рода от функции f(х) и

обозначают .

Таким образом, по определению 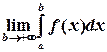. (1)

Если предел, стоящий в правой части равенства (1) существует и конечен, то несобственный интеграл называется сходящимся, в противном случае – расходящимся.

Аналогично определяется несобственный интеграл на промежутке :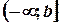

. (2)

Несобственный интеграл с двумя бесконечными пределами определяется формулой:

, (3)

где с– любая фиксированная точка оси Ох.

При этом интеграл называется сходящимся, если сходятся оба несобственных интеграла, стоящих в правой части равенства (3).

Если хотя бы один из интегралов, входящих в правую часть (3), расходится, то несобственный интеграл называется расходящимся.

 

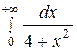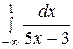Пример 1. Вычислить несобственный интеграл или установить его расходимость: а); б) ; в).

Решение.

 

а)

.

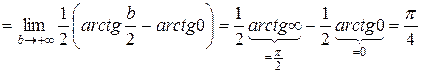Следовательно, интеграл сходится.

б)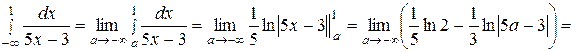

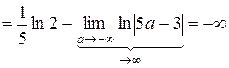. Следовательно, интеграл расходится.

в)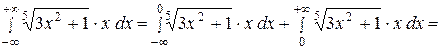

интеграл расходится

интеграл расходится

Следовательно, исходный интеграл расходится.