Предел и непрерывность функций нескольких переменных

 

Для функции двух (и большего числа) переменных вводится понятие предела функции и непрерывности, аналогично случаю функции одной переменной. Введём понятие окрестности точки.

Определение 1:Множество всех точек М(х; у) плоскости, координаты которых удовлетворяют неравенству 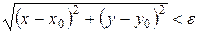называется e–окрестностью точки М₀(х₀; у₀). Другими словами, e-окрестность точки М₀ – это все внутренние точки круга с центром М₀ и радиусом e.

 

Определение 2:Пусть функция z=ƒ(х; у) определена в некоторой окрестности точки М₀(х₀; у₀), кроме, быть может, самой этой точки. Число А называется пределом функции z=ƒ(х; у) при х→х₀ и у→у₀ (или, что то же самое, при М(х; у)→М₀(х₀; у₀), если для любого є>0 существует d>0 такое, что для всех х≠х₀ и у≠у₀ и удовлетворяющих неравенству 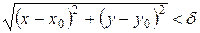выполняется неравенство |ƒ(х; у)–А|<є. Записывают:

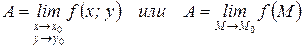
Из определения следует, что если предел существует, то он не зависит от пути, по которому М стремится к М₀ (число таких направлений бесконечно; в частности для функции одной переменной х→х₀ по двум направлениям: справа и слева).

 

Геометрический смысл предела функции двух переменных состоит в следующем: каково бы ни было число e>0, найдется d–окрестность точки М₀(х₀; у₀), что во всех её точках М(х; у), отличных от М₀(х₀; у₀), аппликаты соответствующих точек поверхности z=ƒ(х; у) отличаются от числа А по модулю меньше, чем на e.

 

Предел функции двух переменных обладает свойствами, аналогичными свойствам предела функции одной переменной. Это означает, что справедливы утверждения: если функции ƒ(М) и g(М) определены на множестве D и имеют в точке М₀ этого множества пределы А и В соответственно, то и функции ƒ(М)±g(M), ƒ(М)·g(М), ƒ(М)/g(М), имеют в точке М₀ пределы, которые соответственно равны А±В, А·В, A/B (В≠0).

 

Определение 3:Функция z=ƒ(х; у) (или f(М)) называется непрерывной в точке М₀(х₀; у₀), если она:

а) определена в этой точке и некоторой её окрестности,

б) имеет предел ,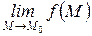

в) этот предел равен значению функции z в точке М₀, т. е.:

 

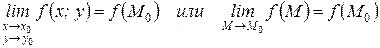
Определение 4:Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области. Точки, в которых непрерывность нарушается (не выполняется хотя бы одно из условий непрерывности функции в точке), называются точками разрыва этой функции. Точки разрыва z=ƒ(х; у) могут образовывать целые линии разрыва. Например, функция 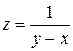имеет линию разрыва у=х.

 

Можно дать другое, равносильное приведённому выше, определение непрерывности функции z=ƒ(х; у) в точке.

 

Определение 5:Обозначим Δх=х–х₀, Δу=у–у₀, Δz=ƒ(х; у)–ƒ(х₀; у₀). Величины Δх и Δу называются приращениями аргументов х и у, а Δz – полным приращением функции ƒ(х; у) в точке М₀(х₀; у₀).

 

Определение 6:Функция z=ƒ(х; у) называется непрерывной в точке М₀(х₀; у₀)ÎD, если выполняется равенство 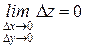т. е. полное приращение функции в этой точке стремится к нулю, когда приращения её аргументов х и у стремятся к нулю.

 

Пользуясь определением непрерывности и теоремами о пределах — арифметические операции над непрерывными функциями и построение сложной функции из непрерывных функций приводит к непрерывным функциям.