Частные производные

 

Частные производные первого порядка:

 

Пусть функция z=ƒ(х; у) определена в области D и (х₀; у₀)ÎD. Тогда при малых |Δх| определено её частное приращение по х: Δ_xz=f(x₀+Δx, y₀)–f(x₀, y₀).

 

Определение 1: Частной производной функции z=ƒ(х; у) по переменной х в точке (х₀; у₀) называют предел (если он существует) отношения частного приращения Δ_xz по х к приращению Δх при стремлении Δх к нулю.

Частная производная по х от функции z=ƒ(х; у) обозначается одним из символов:

Итак, по определению:

Частная производная по х от функции z=ƒ(х; у) в точке М₀(х₀; у₀) обозначается: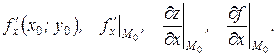

 

Аналогично определяется частная производная по у и вводятся её обозначения:

Частная производная – это производная функции одной переменной, когда значение другой переменной фиксировано. Поэтому частные производные вычисляются по тем же правилам, что и вычисление производных функций одной переменной.

 

Напомним, что для функции одной переменной y=f(x) выражение – означает, что производная у по аргументу х равна отношению дифференциала переменной у к дифференциалу переменной х.

**Для функции двух переменных z=ƒ(х; у) выражение – означает, что частная производная z по аргументу х (z¢_x) равна отношению частного дифференциала переменной z (d_xz) к дифференциалу переменной х (dx).

**Выражение – нужно рассматривать как неразделимый символ частной производной, а не как отношение дифференциалов.

 

Частные производные второго порядка:

 

Частными производными второго порядка от функции z=ƒ(х; у) называются частные производные от частных производных первого порядка.

Определение 2: Частными производными второго порядка функции z=ƒ(х; у) по х и по у соответственно называются:

Определение 3: Смешанными частными производными второго порядка функции z=ƒ(х; у) соответственно называются:

Теорема (Шварца): Если в некоторой окрестности точки М₀(х₀; у₀) функция z=ƒ(х; у) имеет смешанные частные производные 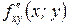и , причём эти производные непрерывны в точке М₀(х₀; у₀), то они равны в этой точке:

Если последнее равенство выполняется, то говорят, что смешанные частные производные 2-го порядка функции z=ƒ(х; у) не зависят от порядка дифференцирования в точке М₀.