Лекция 7. Непрерывность функции

Лекция 7. Непрерывность функции.

Непрерывность функции в точке.

Определение 1: Функция f(x) называется непрерывной в точке х0, если предел функции и её значение в этой точке равны, т. е. Это означает выполнение трёх условий:

Классификация точек разрыва

Определение 1: Точка х₀ называется точкой разрыва функции f(x), если f(x) в точке х₀ не является непрерывной.

 

Напомним, что для непрерывности функции f(x) в точке х₀, необходимо выполнение следующих трёх условий:

1.) функция f(x) определена в точке х₀ и в её окрестности;

2.) функция f(x) имеет предел, при х®х₀;

3.) предел функции в точке х₀ равен значению функции в этой точке.

 

Разрывы функций классифицируются следующим образом.

 

Разрыв первого рода.

Определение 2: Точка х₀ называется точкой разрыва первого рода функции f(x), если в этой точке функция f(x) имеет конечные правый и левый пределы и

а) если правый и левый пределы равны друг другу, но не равны значению функции f(x) в этой точке, то х₀ называется точкой устранимого разрыва.

б) если правый и левый пределы не равны друг другу, то х₀ называется точкой конечного разрыва и имеет место скачок функции.

Скачок функции находится по формуле:

 

Разрыв второго рода.

Определение 3: Точка х₀ называется точкой разрыва второго рода функции f(x), если в этой точке функция f(x) не имеет по крайней мере одного из односторонних пределов, или хотя бы один из односторонних пределов бесконечен.

 

Например: пусть х₀=2

 

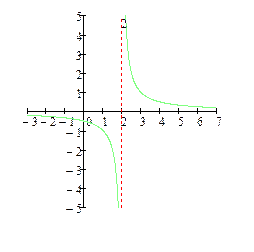
	1) – 2) – 3) –		1) – 2) – 3) –
функция f(x) определена в окрестности точки х0, но не определена в точке х0; разрыв II рода;	функция f(x) определена в окрестности точки х0, но не определена в точке х0; разрыв I рода; точка конечного разрыва; скачок равен 2
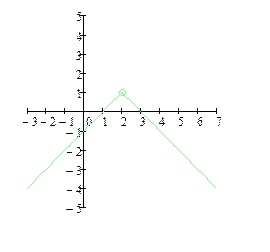
	1) – 2) + 3) –		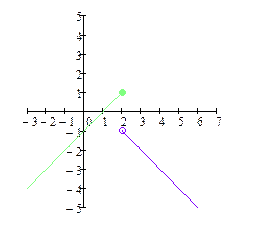1) + 2) – 3) –
функция f(x) определена в окрестности точки х0, но не определена в точке х0; разрыв I рода; точка устранимого разрыва;	функция f(x) определена точке х0, и в её окрестности; разрыв I рода; точка конечного разрыва; скачок равен 2
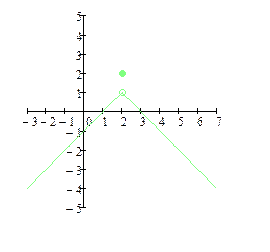
	1) + 2) + 3) –		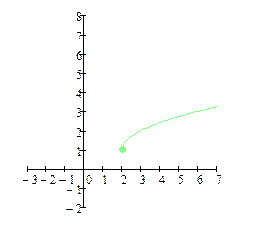1) – 2) – 3) –
функция f(x) определена точке х0, и в её окрестности; разрыв I рода; точка устранимого разрыва;	функция f(x) определена точке х0, но не определена в её окрестности; разрыв II рода;
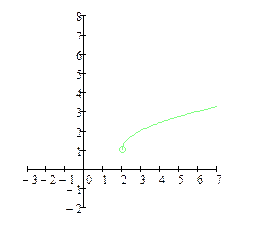
	1) – 2) – 3) –
функция f(x) не определена ни в точке х0, ни в её окрестности; разрыв II рода;

 

Непрерывность функции на промежутке.

Определение 1: Функция f(x) называется непрерывной в интервале (а; b), если она непрерывна в каждой точке этого интервала. Определение 2: Функция f(x) называется непрерывной на отрезке [а; b], если она непрерывна в каждой точке интервала (а;…

Всякая элементарная функция непрерывна на своей области определения.

Теорема 1: (об устойчивости знака непрерывной функции) Пусть функция f(х) непрерывна в точке х0 и f(х0)¹0. Тогда существует d>0 такое, что…   Теорема 2: (I теорема Больцано-Коши) Пусть функция f(х) непрерывна на отрезке [а; b] и на концах отрезка имеет…