Дифференциалы высших порядков.
Определение 1: Пусть функция f(х) дифференцируема в каждой точке х некоторого промежутка, тогда её дифференциал dy=f¢(х)dх, назовём дифференциалом первого порядка.
Итак, dy является функцией двух переменных: аргумента х и его дифференциала dx.
Пусть функция f¢(х), в свою очередь, дифференцируема в некоторой точке х. Будем рассматривать dx в выражении для dy как постоянный множитель. Тогда функция dy представляет собой функцию только аргумента х и её дифференциал в точке х имеет вид:
d(dy)=d[f¢(х)dх]=[f¢(х)dх]¢dх=f²(х)dxdx=f²(х)(dx)2.
Определение 2: Дифференциал от дифференциала dy (обозначим, как d(dy)) в некоторой точке х, называется дифференциалом второго порядка функции f(х) в точке х и обозначается d2y, т. е.
d2y=f²(х)(dx)2
d2y=f²(х)dx2.
Определение 3: Дифференциал от дифференциала d2y (обозначим, как d(d2y)) в некоторой точке х, называется дифференциалом третьего порядка функции f(х) в точке х и обозначается d3y, т. е.
d3y=f²¢(х)(dx)3
d3y=f²¢(х)dx3.
Определение 4:Дифференциал от дифференциала dn-1y (обозначим, как d(dn-1y)) в некоторой точке х, называется дифференциалом n-го порядка функции f(х) в точке х и обозначается dny, т. е.
dny=f(n)(х)(dx)n
dny=f(n)(х)dxn.
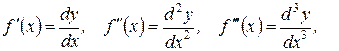
т. е. производную функции можно рассматривать как отношение её дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной.