Производные и дифференциалы высших порядков
Пусть функция f(x) определена и дифференцируема на некотором промежутке X, тогда ее производная  (x) также является функцией от x на этом промежутке. Если
(x) также является функцией от x на этом промежутке. Если  (x) имеет производную на промежутке X, то эта производная называется производной второго порядкафункции y = f(x) и обозначается: y'' или
(x) имеет производную на промежутке X, то эта производная называется производной второго порядкафункции y = f(x) и обозначается: y'' или  (x).
(x).
Итак,  (x) = (
(x) = ( (x))'.
(x))'.
Производная от производной второго порядка называетсяпроизводной третьего порядка и обозначается: y''' или  (x).
(x).
Вообще, производной n-го порядка называется производная от производной
(n – 1)-го порядка и обозначается: y(n) или f (n)(x). Итак, f (n)(x) = (f (n-1)(x))'.
Производные y'', y''', ... называются производными высших порядков.
Пример 1. f (x) =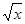 . Найти
. Найти  (x) и
(x) и  (4).
(4).
Решение. 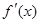 =
=  =
=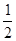
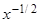 ,
,  (x) = –
(x) = –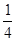
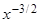 ,
,  (x) =
(x) = 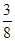
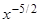 =
= 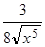 ,
,
 (4) =
(4) = 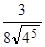 =
=  =
= 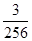 .
.
Пример 2. Найти производную n-го порядка для функции y = e3x.
Решение. y' = 3e3x, y'' = 3× 3e3x = 32e3x, y''' = 33e3x.
По аналогии находим: y(n) = 3ne3x.
Рассмотрим механический смысл второй производной.
Пусть путь S, пройденный телом по прямой за время t, выражается формулой
S = f(t). Известно, что при этом скорость V в момент времени t равна производной от пути по времени: V = 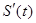 . В момент времени t + Dt скорость получит приращение
. В момент времени t + Dt скорость получит приращение
DV = V(t + Dt) – V(t).
Отношение 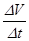 называется средним ускорением за время Dt. Ускорением a в данный момент времени называется предел среднего ускорения, когда Dt ® 0:
называется средним ускорением за время Dt. Ускорением a в данный момент времени называется предел среднего ускорения, когда Dt ® 0:
a = 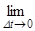
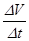 , т.е. a = V'(t) = (S(t))' = S''(t).
, т.е. a = V'(t) = (S(t))' = S''(t).
Следовательно, ускорение при прямолинейном движении равно второй производной от пути по времени: a = S''(t).
Перейдем к рассмотрению дифференциалов высших порядков.
Пусть y = f(x), xÎX. Дифференциал этой функции y = f'(x)dx является функцией от x (если x – не фиксированное число), dx – приращение аргумента x, оно не зависит от x.
Дифференциал от дифференциала функции называется дифференциалом второго порядка и обозначается d2y или d2f(x).
Итак, d2y = d(dy), но dy= 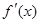 dx, поэтому
dx, поэтому
d2y = d(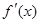 dx) = (
dx) = (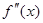 dx)dx =
dx)dx = 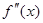 (dx)2.
(dx)2.
Будем вместо (dx)2 писать dx2.
Дифференциалом третьего порядка называется дифференциал от дифференциала второго порядка и обозначается d3y или d3f(x):
d3y = d(d2y) = d(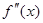 dx2) =
dx2) = 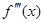 dx3 и т.д.
dx3 и т.д.
Дифференциалом n-го порядка называется дифференциал от дифференциала
(n – 1)-го порядка dny = d(dn – 1y) = d(f (n – 1)(x)dxn – 1) = f (n)(x)dxn.
Итак, dny = f (n)(x)dxn. Отсюда f (n)(x) = 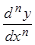 .
.
Заметим, что выражение производной через отношение дифференциалов часто бывает удобно, поэтому оно широко используется. Так, вместо  будем писать:
будем писать:  , вместо
, вместо 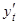 пишем:
пишем: 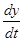 .
.
Пример 3. Найти d3y для функции y = cos2x.
Решение. d3y = y'''dx3. Вычислим y''', находя последовательно y', y'', y''':
y' = (cos2x)' = –2cosxsinx = –sin2x, y'' = (–sin2x)' = –2cos2x, y''' = 4sin2x.
Следовательно, d3y = 4sin2xdx3.
Рассмотрим нахождение производных высших порядков для функций, заданных параметрически и неявно.
Пусть функция y, зависящая от x, задана параметрически уравнениями
 , tÎT
, tÎT
(T – некоторый промежуток).
Найдем  . Известно, что
. Известно, что  =
=  =
= 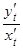 (разд.2.6), поэтому
(разд.2.6), поэтому
 =
= 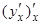 =
= 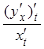 =
=  =
=  .
.
Аналогично будут вычисляться 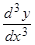 и т.д.
и т.д.
Пример 4. Функция y от x задана параметрически уравнениями:
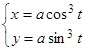 , 0£ t £ p.
, 0£ t £ p.
Найти  .
.
Решение.  =
=  =
= 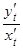 =
= 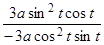 = –tgt;
= –tgt;
 =
= 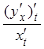 =
=  = -
= - =
= 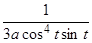 .
.
Нахождение производных высших порядков от функций, заданных неявно, рассмотрим на примере.
Пример 5. Найти  ,
,  для функции, заданной неявно уравнением:
для функции, заданной неявно уравнением:
ey + xy = e. Вычислить y'(0), y''(0).
Решение. Найдем сначала y', как описано в в разд. 2.5:
(ey + xy)' = (e)', ey×y' + y + xy' = 0, y'(ey + x) = –y, y' = –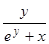 .
.
Для нахождения y'' будем дифференцировать равенство ey×y' + y + xy' = 0, получим:
ey×(y')2 + ey×y'' + y' + y' + xy'' = 0, отсюда найдем y'', затем подставим найденное значение y': y''(ey + x) = –ey×(y')2 – 2y',
y'' = –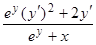 =
= 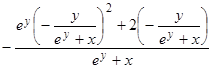 =
= 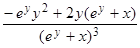 =
=
=  .
.
Итак, y' = – , y'' =
, y'' =  . Подставим x = 0 в исходное уравнение ey + xy = e, получим: ey + 0×y = e, откуда y = 1, значит,
. Подставим x = 0 в исходное уравнение ey + xy = e, получим: ey + 0×y = e, откуда y = 1, значит,
y(0) = 1; y'(0) = –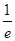 ; y''(0) =
; y''(0) = 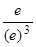 =
= 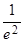 .
.