Решение

Если (x₀) существует, то говорят, что функция f (x) дифференцируема в точке x₀. Установим связь между дифференцируемостью функции f (x) в точке x₀ и ее непрерывностью в этой точке. Напомним, что функция f (x) непрерывна в точке x₀, если она определена в точке x₀ и некоторой ее окрестности, и выполняется равенство:

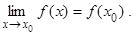
Переформулируем это определение, используя понятия приращения аргумента и приращения функции. Из этого равенства получаем:

. (*)

Другими словами, функция f (x) непрерывна в точке x₀, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

Теорема. Если функция f(x) дифференцируема в точке x₀, то она непрерывна в этой точке.

Доказательство. Дано, что f'(x₀) существует, т.е. 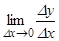есть некоторое число. Покажем, что выполняется равенство (*):

Итак, доказано, что f(x) непрерывна в точке x₀.

Замечание. Если в точке x₀ функция f (x) непрерывна, то в этой точке функция может и не иметь производной, что подтверждается следующим примером.

Пример 2. Функция f(x) = | x | непрерывна в точке x₀ = 0, так как .

Покажем, что эта функция не имеет производной в точке x₀:

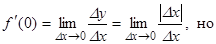
не существует, т.е. f(x) не дифференцируема в точке x₀ = 0.

Рассмотрим геометрический смысл производной.

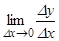На рис. 2.1 изображен график непрерывной функции y = f (x). Точка M₀ на графике имеет координаты x₀, f(x₀), другая точка графика M – координаты x₀ + Dx, f(x₀ + Dx). Прямая M₀M является секущей для линии y = f(x), она наклонена к оси Ox под углом b. Пусть (x₀) существует, т.е. есть некоторое число. Из DM₀MА получаем: (известно, что tgb – угловой коэффициент прямой M₀M). Если Dx ® 0, то точка M движется по графику функции y = f(x), приближаясь к точке M₀, при этом секущая M₀M, поворачиваясь вокруг точки M₀, стремится занять предельное положение, т.е. совпасть с касательной M₀K, при этом 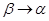(a – угол между касательной M₀K и осью Ox), tgb ® tga.

Таким образом, но tga = k есть угловой коэффициент касательной M₀K.

Итак, угловой коэффициент касательной к графику y = f (x) в точке с абсциссой x₀ равен производной функции f(x) в точке x₀: (x₀) = k = tga.

В этом состоит геометрическое истолкование производной. Очевидно, что уравнение касательной M₀K имеет вид: y – f (x₀) = (x₀)(x – x₀).

Переходим к рассмотрению механического смысла производной.

Пусть материальная точка движется прямолинейно неравномерно по закону S = f(t), где t – время, S – путь, проходимый точкой за время t.

Пусть в момент времени t₀ точка находилась в положении M₀ (рис. 2.2). Поставим задачу: определить скорость материальной точки в момент t₀. Рассмотрим другой момент времени
t₀ + Dt. За время t₀ пройденный точкой путь равен: S₀ = f (t₀), за (t₀ + Dt) пройдено расстояние S = f(t₀ + Dt), и точка оказалась в положении M, тогда за время Dt пройден путь M₀M и он равен:

S – S₀ = f(t₀ + Dt) – f(t₀) = DS.

Средняя скорость V_ср за пpомежуток времени Dt равна: Но средняя скорость может быть различной, в зависимости от промежутка времени Dt. Скоростью в момент времени t₀ (обозначим V(t₀)) называется предел средней скорости V_ср при Dt ® 0. Итак,

Вывод. Производная от пути S = f(t) в момент времени t₀ есть скорость в момент времени t₀.