Доказательство
Так как Du = u(x + Dx) – u(x), то u(x + Dx) = u(x) + Du.
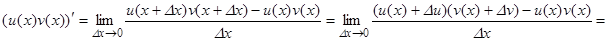 |
Аналогично, v(x + Dx) = v(x) + Dv.
 |
Следствие. Постоянный множитель можно выносить за знак производной, т.е.
(C×f(x))' = C× (x).
(x).
Доказательство. Пусть C – постоянное число, тогда (C)' = 0. По теореме 2:
(C×f(x))' = (C)'×f(x) + C× (x) = 0×f(x) + C×
(x) = 0×f(x) + C× (x) = C×
(x) = C× (x).
(x).
В частности, (u(x) – v(x))' = (u(x) + (–1)×v(x))' = u'(x) + (–1)×v'(x) = u'(x) – v'(x),
т.е. (u(x) – v(x))' = u'(x) – v'(x) (производная разности двух функций равна разности их производных).
Теорема 3. Если функции u(x), v(x) дифференцируемы в точке x и v(x) ¹ 0, то их частное дифференцируемо в этой точке, причем
 |
Доказательство
 |
Заметим, что, так как v(x) дифференцируема в точке x, а, следовательно, непрерывна в точке x, то
 . Тогда:
. Тогда:
С помощью теоремы 3 можно вычислить производные функций tgx и ctgx:
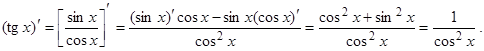 |
Итак, получили формулу:
 .
.
Производная для ctgx находится аналогично (сделайте это): 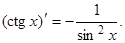
Пусть y = f(j(x)) является сложной функцией, составленной из функции
y = f (u), u = j(x), где u – промежуточный аргумент. Покажем, как найти производную сложной функции, зная производную для функции y = f (u) (ее будем обозначать через 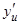 ) и производную
) и производную 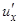 для функции u = j(x).
для функции u = j(x).
Теорема 4. Если функция u = j(x) имеет производную 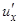 в точке x, а функция
в точке x, а функция
y = f (u) имеет производную 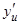 в точке u (u = j(x)), то сложная функция y = f(j(x)) в точке x имеет производную
в точке u (u = j(x)), то сложная функция y = f(j(x)) в точке x имеет производную  , причем
, причем  =
= 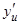
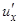 .
.
Иначе, производная сложной функции равна произведению производной данной функции по промежуточному аргументу на производную промежуточного аргумента.
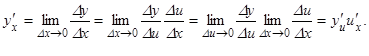 |
Доказательство. Функция u = j(x) дифференцируема в точке x, поэтому непрерывна в этой точке, т.е.
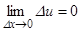 (будем предполагать, что Du ¹ 0), тогда
(будем предполагать, что Du ¹ 0), тогда
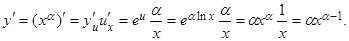 |
С помощью теоремы 4 найдем производную степенной функции y = xa, где
a – постоянное число. По свойствам логарифмов xa = (elnx)a = ealnx, поэтому xa = ealnx является сложной функцией от x: y = eu, u = alnx. По теореме 4:
Итак, получена формула: (xa)' = axa – 1.
Очевидно, производные функций (найденные в разд. 2.2), могут быть вычислены по полученной формуле. В самом деле, например, для функции 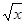 имеем:
имеем:
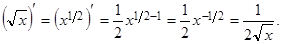
Введем правило для нахождения производной обратной функции.
Теорема 5. Пусть функция y = f(x) определена на промежутке X, непрерывна, монотонна (возрастает или убывает) и дифференцируема на X. Если ее производная  в точке x не равна 0, то обратная функция x = j(y) имеет производную
в точке x не равна 0, то обратная функция x = j(y) имеет производную  в точке y
в точке y
(y = f(x)), причем 
Доказательство. Функция y = f(x) определена, непрерывна и монотонна на промежутке X, тогда по теореме 4 (разд. 1.13) она имеет обратную функцию x = j(y), определенную, непрерывную и монотонную на промежутке Y.
Если значение аргумента y получает приращение Dy, отличное от нуля, то в силу монотонности функции x = j(y) функция x получает приращение Dx и Dx ¹ 0. В силу непрерывности функции x = j(y):  .
.
Следовательно, 
Итак,  Теорема доказана.
Теорема доказана.