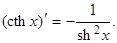Производные обратных тригонометрических и гиперболических функций

Используя теорему 5 (разд. 2.3) докажем следующие формулы:

1) ;

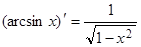2) ;

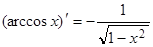3) ;

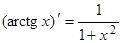4) .

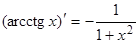1. Если xÎ[–1, 1], yÎ[–p/2, p/2], то функции y = arcsinx, x = siny являются взаимно обратными, причем 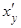= (siny)' = cosy. Если –p/2 < y < p/2 (при этом –1 < x < 1), то
cosy > 0, поэтому .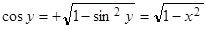

По теореме 5 (разд. 2.3) имеем: 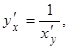тогда

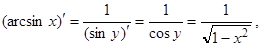(–1 < x < 1).

2. Функции y = arccosx, x = cosy взаимно обратны, если xÎ[–1, 1], yÎ[0, p],
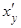= (cosy)' = –siny. Если 0 < y < p (при этом –1 < x < 1), то siny > 0, поэтому

.

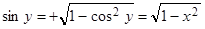Так как 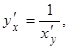то

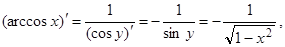(–1 < x < 1).

3. Функции y = arctgx, x = tgy взаимно обратны, если yÎ(–p/2, p/2), a xÎR. Используя равенство 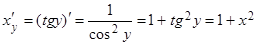, получаем:

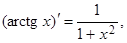xÎR.

4. Для y Î (0, p) функции y = arсctgx, x = сtgy взаимно обратны,
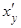= –(1 + ctg²y) = –(1 + x²), поэтому

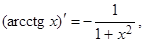xÎR.

Итак, мы вывели формулы производных для обратных тригонометрических функций.

Введем понятия гиперболических функций, имеющих применение в математике и ее приложениях:

гиперболический синус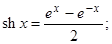

гиперболический косинус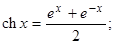

гиперболический тангенс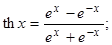

гиперболический котангенс .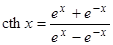

Для гиперболических функций справедливы тождества:

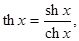
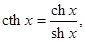ch²x – sh²x =1. (Проверьте это!).

Найдем производные для гиперболических функций, при этом напомним, что
(e^–x)' = e^–x×(–1) = –e^–x (как производная сложной функции):

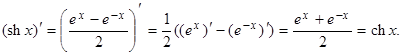
Итак, (shx)' = chx.

Аналогично доказывается, что (chx)' = shx.

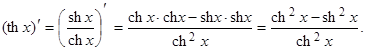
Так как ch²x – sh²x =1, то получаем: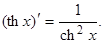

Аналогично можно показать, что