Задача 1.
Найти указанные пределы:
a) 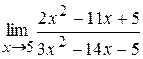 ;
;
b) 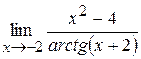 ;
;
c) 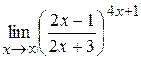 ;
;
d) 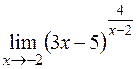 .
.
Решение:
a) Вначале убеждаемся, что предел функции нельзя найти непосредственной подстановкой, что при указанном изменении аргумента она представляет отношение двух бесконечно малых величин (неопределенность вида 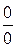 ). Затем делаем преобразования, чтобы сократить дробь на множитель, стремящийся к нулю.
). Затем делаем преобразования, чтобы сократить дробь на множитель, стремящийся к нулю.
Разлагаем числитель и знаменатель на множители. Затем сокращаем дробь на 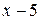 . Аргумент x стремится к своему предельному значению, но не совпадает с ним, поэтому множитель
. Аргумент x стремится к своему предельному значению, но не совпадает с ним, поэтому множитель 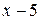 отличен от нуля при
отличен от нуля при 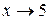 .
.
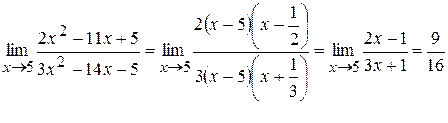 .
.
b) Данная функция не определена в предельной точке и при изменении аргумента она представляет отношение двух бесконечно малых величин (неопределенность вида 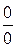 ).
).
Полагая 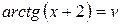 , получаем
, получаем  , когда
, когда 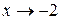 :
:
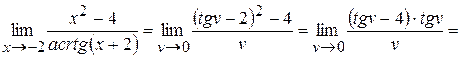

Искомый предел можно найти иначе. Известно, что при нахождении предела отношения двух бесконечно малых величин можно каждую из них (или только одну) заменить другой бесконечно малой, ей эквивалентной.
Так как при 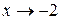
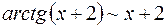 , то
, то
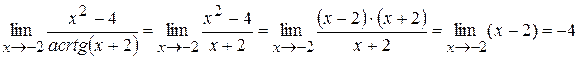 .
.
c) При  основание
основание  стремится к
стремится к 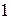 , а показатель степени
, а показатель степени  стремится к бесконечности. Следовательно, имеем неопределенность вида
стремится к бесконечности. Следовательно, имеем неопределенность вида  . Представим основание в виде суммы
. Представим основание в виде суммы 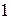 и некоторой бесконечно малой величины:
и некоторой бесконечно малой величины:
 .
.
Тогда
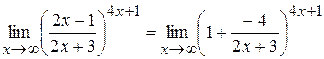 .
.
Положим 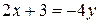 ; при
; при  переменная
переменная 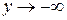 . Выразим показатель степени через новую переменную
. Выразим показатель степени через новую переменную  . Так как
. Так как 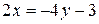 , то
, то 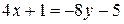 . Таким образом,
. Таким образом,
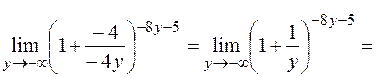

(используем второй замечательный предел).
d) При  основание
основание  стремится к единице, а показатель степени
стремится к единице, а показатель степени 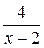 стремится к бесконечности.
стремится к бесконечности.
Положим 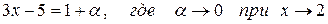 .
.
Тогда
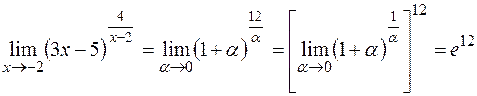 .
.