Задача 8.
Исследовать функцию  и построить ее график.
и построить ее график.
Решение:
1. Определим область существования функции. Квадратный трехчлен, стоящий под знаком логарифма, можно представить так:
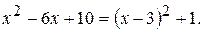 Как видно, под знаком логарифма будет положительное число при любом значении аргумента x. Следовательно, областью существования данной функции служит вся числовая ось.
Как видно, под знаком логарифма будет положительное число при любом значении аргумента x. Следовательно, областью существования данной функции служит вся числовая ось.
2. Исследуем функцию на непрерывность. Функция всюду непрерывна и не имеет точек разрыва.
3. Установим четность и нечетность функции. Так как 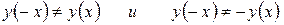 , то функция не является ни четной ни нечетной.
, то функция не является ни четной ни нечетной.
4. Исследуем функцию на экстремум. Находим первую производную:
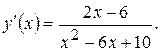
Знаменатель 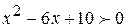 для любого x. Как видно, при
для любого x. Как видно, при 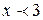 первая производная отрицательна, а при
первая производная отрицательна, а при 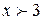 положительна. При
положительна. При  первая производная меняет свой знак с минуса на плюс. В этой точке функция имеет минимум:
первая производная меняет свой знак с минуса на плюс. В этой точке функция имеет минимум:
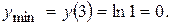
Итак, 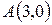 – точка минимума. Функция убывает на интервале
– точка минимума. Функция убывает на интервале  и возрастает на интервале
и возрастает на интервале  .
.
b) Определим точки перегиба графика функции и интервалы выпуклости и вогнутости кривой. Для этого находим вторую производную:
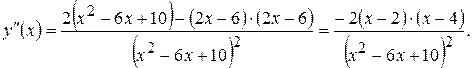
Разобьем всю числовую ось на три интервала: 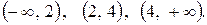 Как видно, в первом и третьем интервалах вторая производная отрицательна, а во втором интервале положительна. При
Как видно, в первом и третьем интервалах вторая производная отрицательна, а во втором интервале положительна. При 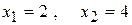 вторая производная меняет знак. Эти значения аргумента являются абсциссами точек перегиба. Определим ординаты этих точек:
вторая производная меняет знак. Эти значения аргумента являются абсциссами точек перегиба. Определим ординаты этих точек:
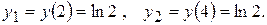
Следовательно, мы получили точки перегиба графика функции - 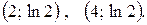 График является выпуклым в интервалах
График является выпуклым в интервалах 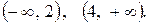 и вогнутым в интервале
и вогнутым в интервале 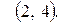
c) Определим уравнения асимптот графика функции. Для определения уравнения асимптоты 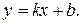 воспользуемся формулами:
воспользуемся формулами:
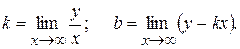
Имеем
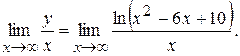
Чтобы найти искомый предел, дважды применяем правило Лопиталя:
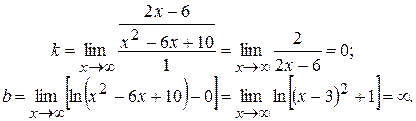
Итак, кривая не имеет асимптот. График исследуемой функции показан на рис.2.
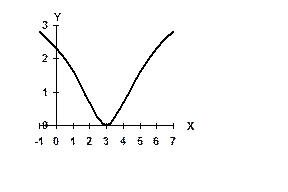
рис.2
Исследовать функцию 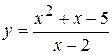 и построить ее график.
и построить ее график.
Решение:
b) Функция терпит разрыв при 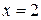 . При всех других значениях аргумента она непрерывна.
. При всех других значениях аргумента она непрерывна.
c) Функция не является ни четной ни нечетной, так как 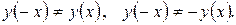
d) Исследуем функцию на экстремум. Используя второй достаточный признак экстремума: если в стационарной точке 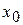 вторая производная отлична от нуля, то в этой точке функция имеет максимум, если вторая производная в этой точке <0, и минимум, если вторая производная в этой точке >0. Находим первую производную:
вторая производная отлична от нуля, то в этой точке функция имеет максимум, если вторая производная в этой точке <0, и минимум, если вторая производная в этой точке >0. Находим первую производную:
 (1)
(1)
или
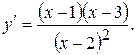
Как видно, первая производная равна нулю при 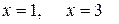 и не существует при
и не существует при 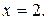 Так как при
Так как при 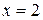 заданная функция не существует. То эта точка не подлежит исследованию. Дифференцируя (1), находим вторую производную:
заданная функция не существует. То эта точка не подлежит исследованию. Дифференцируя (1), находим вторую производную:
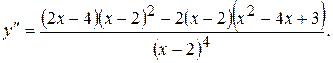
Сократив на 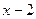 и выполнив преобразования в числителе, получим
и выполнив преобразования в числителе, получим
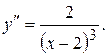 (2)
(2)
Так как 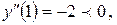 то при
то при 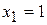 функция имеет максимум. Так как
функция имеет максимум. Так как 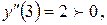 то при
то при 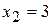 функция имеет минимум.
функция имеет минимум.
Вычислим значения функции в точках экстремума:  Следовательно, точка (1;3) – точка максимума, а точка (3;7) – точка минимума.
Следовательно, точка (1;3) – точка максимума, а точка (3;7) – точка минимума.
b) Из (2) видно, что вторая производная ни при каком значении аргумента не обращается в ноль. Следовательно, график исследуемой функции не имеет точек перегиба.
c) Определим асимптоты графика функции. 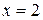 есть уравнение вертикальной асимптоты. Используя соответствующие формулы, выясним вопрос о наличии наклонной асимптоты:
есть уравнение вертикальной асимптоты. Используя соответствующие формулы, выясним вопрос о наличии наклонной асимптоты:
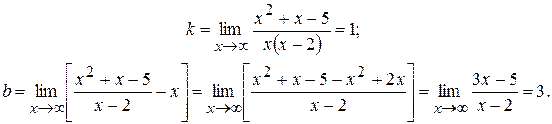
Следовательно, 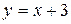 - уравнение наклонной асимптоты. График исследуемой функции приведен на рис.3.
- уравнение наклонной асимптоты. График исследуемой функции приведен на рис.3.
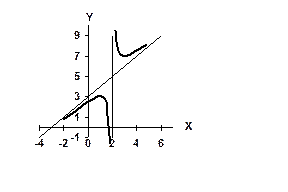
рис.3