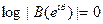Единице

Пусть так что

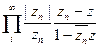
сходится в {|z|< 1} и представляет функцию В(z), аналитическую в этом круге. Согласно элементарной теории функции комплексной переменной, из того, что каждый сомножитель произведения по модулю меньше 1 в {|z|< 1}, вытекает, что В(z)< 1 для |z< 1.

Следовательно, для почти всех ζ, |ζ|=1, предельная функция B(ζ)=limB(z) при z →ζ существует (теарема Фату).

Теорема.|В(е^iθ)|=1 п. в.

Доказательство.

Без ограничения общности можно счи­тать, что все точки z_n отличны от нуля (в противном случае мы рассмотрели бы функцию B(z)/z^k вместо В (z)). Тогда 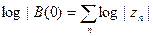Теперь из того, что вытекает, что 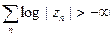. (NB: 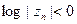для каждого п. Возьмём число r, 0<r< 1, не равное ни одной из величин |z_n |. Тогда в силу простейшей разновидности фор­мулы Йенсена

,

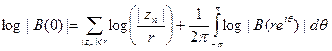т. е.

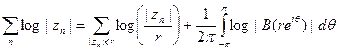
или

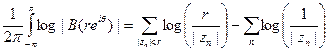
Выберем и зафиксируем какое-нибудь число р, такое что 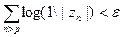, и возьмём r< 1 настолько блнзким к 1, чтобы при п=1,2, ,.., р все точки z_n лежали в круге {z<r}. Тогда из предыдущего соотношения получим

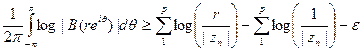
или, если взять r < 1 достаточно близким к 1,

Это значит, что

поскольку число ɛ>0 было произвольным. Но В (re^iθ) →В (е^iθ) п. в. при r→1, и

Следовательно, по лемме Фату (переходим к пределу по последовательности чисел r, стремящихся к 1)

Поскольку 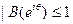, мы получаем, что