Первоначальное изучение граничного поведения
Ядро Пуассона Рr(θ) обладает и четвертым свойством: d) Для любого σ > О
Рr(θ)→0 равномерно для σ≤│θ│≤π при r→1. Это сразу следует из формулы для Рr(θ) .
Теорема. Пусть функция F непрерывна на R и F(t+2π)=F(θ). Пусть

Тогда U(z)→F(φ), когда  , и сходимость равномерна по φ.
, и сходимость равномерна по φ.
Доказательство.
Этот результат восходит к самому Пуассону, который полагал, что отсюда вытекает сходимость ряда Фурье функции к ней самой (на самом деле из теоремы это не следует!). Запишем

Для заданного произвольного числа <р мы имеем по свойству с)
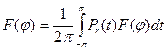
Следовательно,
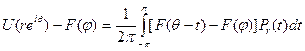
Пусть  таково, что |F(s)— F(φ)|< ε при |s — φ|<2ϭ;
таково, что |F(s)— F(φ)|< ε при |s — φ|<2ϭ;
число ϭ здесь зависит только от ε, а не от φ, из-за (равномерной!) непрерывности функции F.
Запишем интеграл в правой части в виде суммы двух:
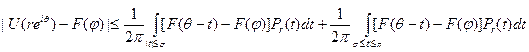
Если |θ-φ|< ϭ то первый интеграл справа не превосходит 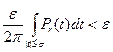
Tb М — верхняя грань величины |F(t)| Тогда второй интеграл не превосходит
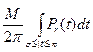
что меньше ε, если r достаточно близко к 1, в силу свойства d).
Таким образом,  , если |θ-φ|< ϭ, а r достаточно близко к 1. Q. E. D.
, если |θ-φ|< ϭ, а r достаточно близко к 1. Q. E. D.
Замечание. Свойства a), b), с) и d) вместе взятые показывают, что  представляет собою так называемую аппроксимативную единицу. Доказанная теорема имеет место в силу этих свойств: не только для ядра Пуассона, но и для других ядер, являющихся аппроксимативными единицами, справедливы аналогичные результаты.
представляет собою так называемую аппроксимативную единицу. Доказанная теорема имеет место в силу этих свойств: не только для ядра Пуассона, но и для других ядер, являющихся аппроксимативными единицами, справедливы аналогичные результаты.
Теорема. Пусть  пусть функция F[t) непрерывна в точке θ0. Тогда
пусть функция F[t) непрерывна в точке θ0. Тогда  стремится к F(θ0) при стремлении reiθ к eiθ
стремится к F(θ0) при стремлении reiθ к eiθ
Доказательство такое же, как у предыдущей теоремы.
Теорема. Пусть 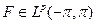 , 1≤ р < ∞ , и пусть
, 1≤ р < ∞ , и пусть

Тогда  , т.е.
, т.е.
стремится к F(G) в А"-норме при r→ 1.
Доказательство.
Положим Fr(θ) = U(re1θ). Тогда

Используя свойства а) и с) (мы рассматриваем  как предел выпуклых комбинаций функций
как предел выпуклых комбинаций функций 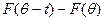 . считая t параметром, а θ — переменной), имеем по очевидному обобщению неравенства треугольника
. считая t параметром, а θ — переменной), имеем по очевидному обобщению неравенства треугольника

Полагая

получим

Но  при
при  0. Это так, потому что сдвиг непрерывен в LP-норме для 1≤р <∞. Это следует а свою очередь из элементарных фактов теории функций вещественной переменной. Действительно, пусть даны
0. Это так, потому что сдвиг непрерывен в LP-норме для 1≤р <∞. Это следует а свою очередь из элементарных фактов теории функций вещественной переменной. Действительно, пусть даны 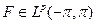 ) и ε > 0. Найдем непрерывную функцию G, периодическую с периодом 2π, такую что ||F — G||p<ɛ. Тогда, очевидно,
) и ε > 0. Найдем непрерывную функцию G, периодическую с периодом 2π, такую что ||F — G||p<ɛ. Тогда, очевидно,
 для |t|<ϭ при достаточно малых σ в силу равномерной непрерывности; следовательно,
для |t|<ϭ при достаточно малых σ в силу равномерной непрерывности; следовательно,
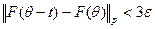 для |t|<σ
для |t|<σ
Во всяком случае, функция Ф(t) непрерывна в 0, где она равна нулю.
Поэтому, по предыдущей теореме,  при r→∞. Q. E. D.
при r→∞. Q. E. D.
При р = ∞ все, что мы имеем, — это ω*-сходимость:
Теорема. Если 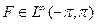 и
и
 ,
,
то 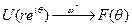 при r→1
при r→1
Доказательство.
Возьмём произвольную функцию  Нужно доказать, что
Нужно доказать, что
при

при r→1 . Но это так, потому что (используем чётность  )
)
 стремится к G(t) при r→1 по предыдущей теореме. Остаётся только применить теорему Фубини.
стремится к G(t) при r→1 по предыдущей теореме. Остаётся только применить теорему Фубини.
Аналогично справедлива
Теорема. Пусть  где μ — конечная вещественная мера на [-π,π]. Тогда
где μ — конечная вещественная мера на [-π,π]. Тогда  при r→1, т. е. для любой непрерывной функции G(θ), периодической с периодом 2π,
при r→1, т. е. для любой непрерывной функции G(θ), периодической с периодом 2π,

когда r→1
Доказательство.
Применяем теорему Фубини вместе с первым результатом этого подпункта.