Линейные однородные уравнения с постоянными коэффициентами
1.2.1. Теоретическая справка
Дифференциальное уравнение 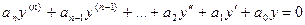 , (2.1)
, (2.1)
где 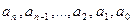 - постоянные величины, называется линейным однородным уравнением
- постоянные величины, называется линейным однородным уравнением 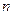 - го порядка с постоянными коэффициентами.
- го порядка с постоянными коэффициентами. , (2.2)
, (2.2)
где  - его линейно независимые частные решения. Последние находятся с помощью характеристического уравнения
- его линейно независимые частные решения. Последние находятся с помощью характеристического уравнения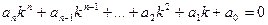 . (2.3)
. (2.3)
Если характеристическое уравнение имеет 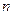 действительных различных корней
действительных различных корней  , то каждому из них соответствует частное решение
, то каждому из них соответствует частное решение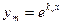 (2.4)
(2.4)
и общее решение уравнения (2.1) принимает вид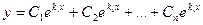 . (2.5)
. (2.5)
Если уравнение (2.3) имеет n действительных равных корней 
 (т.е. корень
(т.е. корень 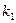 имеет кратность n), то в формуле (2.2) им соответствуют решения
имеет кратность n), то в формуле (2.2) им соответствуют решения . (2.6)
. (2.6)
Однократным комплексно сопряженным корням 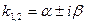
 уравнения (2.3) в формуле (2.2) соответствуют решения:
уравнения (2.3) в формуле (2.2) соответствуют решения: 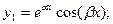
 (2.7)
(2.7)
Комплексно сопряженным корням 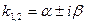 кратности n соответствуют частные решения:
кратности n соответствуют частные решения:
 (2.8)
(2.8)
Частные решения 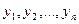 уравнения (2.1) образуют ф.с.р. на интервале
уравнения (2.1) образуют ф.с.р. на интервале  , если ни в одной очке этого интервала определитель Вронского
, если ни в одной очке этого интервала определитель Вронского 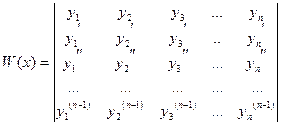 не обращается в нуль (линейно независимы), в противном случае решения не образуют ф.с.р.
не обращается в нуль (линейно независимы), в противном случае решения не образуют ф.с.р.
Пример. Образуют ли функции 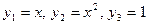 ф.с.р. дифференциального уравнения третьего порядка?
ф.с.р. дифференциального уравнения третьего порядка?
>> a=[x x^2 1];
>> det([a;diff(a);diff(a,x,2)])
ans = 2
Функции roots( )и poly( )
Функции предназначены, соответственно , для вычисления корней полинома и его восстановления по значениям корней. Эти функции имеют вид: roots( Р ), poly( r ), где Р – вектор коэффициентов полинома; r – вектор корней полинома.
Пример.Как выглядит ЛОДУ 2-го порядка, если корни характеристического уравнения  .
.
Решение:
>> poly([2+5i,2-5i])
ans = 1 -4 29
Имеем характеристическое уравнение  и ЛОДУ
и ЛОДУ 
Пример. Найти корни уравнения 
>> roots([1 -4 8 -8 4])
ans =
1.0000 + 1.0000i
1.0000 - 1.0000i
1.0000 + 1.0000i
1.0000 - 1.0000i