Линейные неоднородные уравнения с постоянными коэффициентами
1.3.1. Теоретическая справка
Дифференциальное уравнение
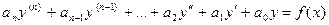 (3.1)
(3.1)
называется линейным неоднородным уравнением с постоянными коэффициентами 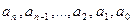 .
.
Если 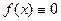 , то уравнение (3.1) становится однородным:
, то уравнение (3.1) становится однородным:
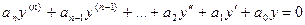 . (3.2)
. (3.2)
Общее решение уравнения (3.1) определяется формулой
 , (3.3)
, (3.3)
где 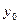 - общее решение соответствующего однородного уравнения (3.2), а
- общее решение соответствующего однородного уравнения (3.2), а  - частное решение данного неоднородного уравнения.
- частное решение данного неоднородного уравнения.
В простейших случаях частное решение может быть найдено с помощью метода неопределенных коэффициентов. Если  , (3.4)
, (3.4)
где  - многочлен степени
- многочлен степени 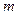 , то частное решение ищут в виде
, то частное решение ищут в виде
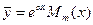 , (3.5)
, (3.5)
где 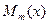 - многочлен той же степени
- многочлен той же степени  с неопределенными коэффициентами, если
с неопределенными коэффициентами, если 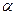 не является корнем характеристического уравнения, соответствующего уравнению (3.2), и в виде
не является корнем характеристического уравнения, соответствующего уравнению (3.2), и в виде
 , (3.6)
, (3.6)
если 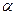 - корень указанного уравнения кратности
- корень указанного уравнения кратности 
В частности, при 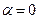
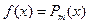 и если
и если 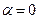 не является корнем характеристического уравнения, то существует частное решение
не является корнем характеристического уравнения, то существует частное решение 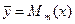 , если
, если 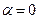 - корень характеристического уравнения кратности
- корень характеристического уравнения кратности  , то
, то 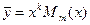 .
.
Если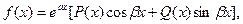 (3.7)
(3.7)
где 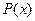 и
и 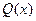 - многочлены, наибольшая степень которых
- многочлены, наибольшая степень которых 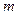 , то частное решение ищут в виде
, то частное решение ищут в виде
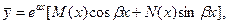 (3.8)
(3.8)
если  не является корнем характеристического уравнения, и в виде
не является корнем характеристического уравнения, и в виде
 (3.9)
(3.9)
где  и
и 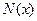 - многочлены степени
- многочлены степени 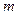 , если
, если  - корень указанного уравнения кратности
- корень указанного уравнения кратности  .
.
Если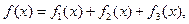 (3.10)
(3.10)
где 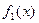 ,
, 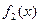 ,
, 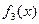 - функции вида (3.4) и (3.7), то существует частное решение
- функции вида (3.4) и (3.7), то существует частное решение
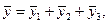 (3.11)
(3.11)
определяемое указанными выше правилами.
В общем случае частное решение уравнения (3.1) может быть найдено с помощью метода вариации произвольных постоянных (метода Лагранжа). Если 
общее решение однородного уравнения (3.2), то общее решение неоднородного уравнения (3.1) ищут в виде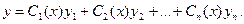 (3.12)
(3.12)
Функции 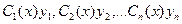 находят из системы уравнений:
находят из системы уравнений:
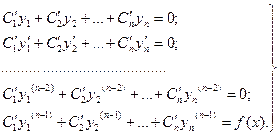 (3.13)
(3.13)
Пример 3.1. Решить уравнение 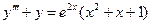 .
.
Решение. Это линейное неоднородное уравнение третьего порядка с постоянными коэффициентами, правая часть которого есть функция вида (3.4), где 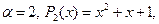 т.е.
т.е. 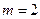 .
.
Найдем сначала общее решение соответствующего однородного уравнения 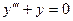 .
.
Так как характеристическое уравнение 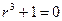 имеет корни
имеет корни 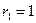 ,
, 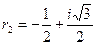 ,
, 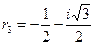 , то общее решение однородного уравнения определяется формулой
, то общее решение однородного уравнения определяется формулой
 .
.
В соответствии с формулой (3.5) частное решение исходного уравнения ищем в виде
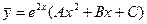 ,
,
поскольку число 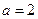 не является корнем характеристического уравнения
не является корнем характеристического уравнения 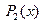 - многочлен второй степени.
- многочлен второй степени.
Находим производные функции 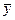 :
:
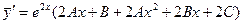 ;
;
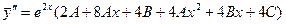 ;
;
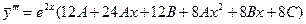 .
.
Подставляя выражения для 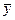 и
и 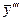 в данное уравнение и сокращая на
в данное уравнение и сокращая на 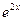 , получим тождество
, получим тождество
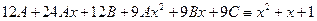 ,
,
откуда
и 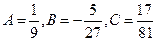 ,
,
поэтому  .
.
Общее решение данного уравнения имеет вид
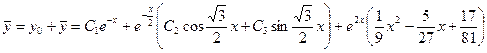 .
.
Решение в MATLAB
>> dsolve('D3y+y=(e^2*t)*(t^2+t+1)')
Решение в Matlab
ans = -6*e^2+e^2*t+e^2*t^2+e^2*t^3+C1*exp(-t)+C2*exp(1/2*t)*sin(1/2*3^(1/2)*t)+C3*exp(1/2*t)*cos(1/2*3^(1/2)*t)
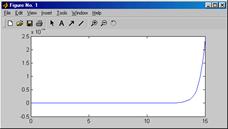
>> y0=[-0.1 -1 1];
>> tspan=[0 15];
>> [t,y]=ode45('ex31',tspan,y0);
>> plot(t,y(:,1))