Решения дифференциальных уравнений численными методами в среде Matlab.

В MATLAB имеется целый ряд встроенных функций, предназначенных для решения зада­чи Коши для обыкновенных дифференциальных уравнений. Это такие функции, как ode45, ode23, odell3, odel5s, ode23s, ode23t и ode23tb. Их еще называют солверами (от англ. слова solver, которое переводится как "решатель").

В перечисленных функциях реализованы различные методы решения дифференциальных уравнений, поэтому выбор той или иной функции зависит от характеристик решаемой задачи.

Понятие: Система называется жёсткой если возможна потеря точности в процессе численного решения, т.к. на разных отрезках изменения независимых переменных решения ведут себя по-разному: в одних местах наблюдается очень быстрое изменение независимых переменных, в то время как в других местах очень медленное.

Решатели реализуют следующие методы решения систем дифференциальных уравнений, причем для решения жестких систем уравнений рекомендуется использовать только специальные решатели ode 15s , ode23s, ode23t. ode23tb:

· ode45 — одношаговые явные методы Рунге-Кутта 4-го и 5-го порядка. Это классический метод, рекомендуемый для начальной пробы решения. Во многих случаях он дает хорошие результаты;

· ode23 — одношаговые явные методы Рунге-Кутта 2-го и 4-го порядка. При умеренной жесткости системы ОДУ и низких требованиях к точности этот метод;. может дать выигрыш в скорости решения;

· ode113 — многошаговый метод Адамса-Башворта-Мултона переменного порядка Это адаптивный метод, который может обеспечить высокую точность решения

· ode23tb — неявный метод Рунге-Кутта в начале решения и метод, использующий формулы обратного дифференцирования 2-го порядка в последующем.Несмотря на сравнительно низкую точность, этот метод может оказаться более эффективным, чем ode15s;

· ode15s — многошаговый метод переменного порядка (от 1 до 5, по умолчанию 5), использующий формулы численного дифференцирования. Это адаптивный метод, его стоит применять, если решатель ode45 не обеспечивает решения;

· ode23s — одношаговый метод, использующий модифицированную формулу Розенброка 2-го порядка. Может обеспечить высокую скорость вычислений при низкой точности решения жесткой системы дифференциальных уравнений;

· ode23t — метод трапеций с интерполяцией. Этот метод дает хорошие результаты при решении задач, описывающих колебательные системы с почти гармоническим выходным сигналом;

 

В самом простом случае синтаксис вызова перечисленных выше функций один и тот же.

[t, Y]=solver(@F,tspan,yO)

 

Здесь solver— название соответствующего солвера (например, ode45 или ode23), t — вектор-столбец, содержащий значения независимой переменной (обычно это значения време­ни), Y— массив решений, каждая строка которого соответствует определенному элементу вектора t. Аргумент @F — это указатель на функцию, которая вычисляет правые части сис­темы дифференциальных уравнений (в частности, имя файл-функции в одинарных кавычках), tspan — вектор, определяющий интервал интегрирования (можно задать и промежуточные значения), а уО — скаляр или вектор-столбец, в котором задаются начальные условия; относительная погрешность RelTol (по умолчанию le-З), абсолютная погрешность AbsTol (все компоненты по умолчанию равны 1е-6);

Пример: Решить уравнение 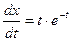в интервале с начальным условием .

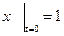Решение:

1.Создаём m-файл

function f=pr1(t,x)

f=t*exp(-t);

2.Сохраняем под именем pr1.

3. Вызываем в командной строке

>> [T,X]=ode45('pr1',[0, 0.5], [1]);

% [0, 0,5 ] – интервал на котором необходимо получить решение.

% [1] – начальное значение решения

>> plot(T,X)

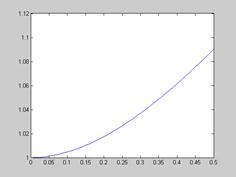
>>[T X] % выводим значения Т и Х

 

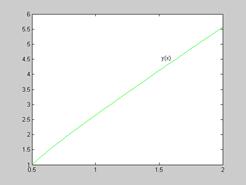
Пример: Получить аналитическое и численное решение дифференциального уравнения: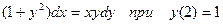

На графике общего решения указать частное.

Решение:

>> y=dsolve('Dy=(1+y^2)/(x*y)','x')

y =

[ (-1+x^2*C1)^(1/2)] % общее решение

[ -(-1+x^2*C1)^(1/2)]

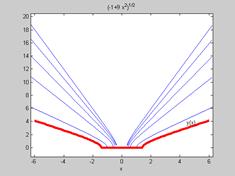
>> syms x C1,y=(-1+x^2*C1)^(1/2); % построение общего решения

>> for C1=1:2:9

y=(-1+x^2*C1)^(1/2);

ezplot(y), hold on

end

>> y1=dsolve('Dy=(1+y^2)/(x*y)','y(2)=1','x')

y1 = (-1+1/2*x^2)^(1/2) % частное решение

>> x=-6:0.1:6;

>> y1=(-1+1/2*x.^2).^(1/2);

>> h=plot(x,y1,'r')

>> set(h,'LineWidth',4)

>> gtext('y(x)')

 

% нахождение численного решения

1. созданиём файл-функцию, в которую записываем правую часть уравнения:

function dydx=F(x,y)

dydx=zeros(1,1);

dydx(1)=(1+y^2)/(x*y);

1. Сохраняем под именем F.m
2. Для получения численного решения в окне команд набираем:

>> [x y]=ode45(@F,[0.5 2],[1]);

% дескриптор @ обеспечивает связь с файл-функцией правой части.

>> plot(x,y,'g')

>> hold on; gtext('y1(x)')

% нанесение надписи

>> [x y ]