Дискретная интерпретация операционного исчисления Микусиньского
Как известно, операционное исчисление, позволяющее сводить дифференциальные задачи к алгебраическим, возникло благодаря работам английского ученого Оливера Хевисайда (1859-1925), который предложил формальные правила обращения с дифференциальным оператором  и некоторыми функциями от этого оператора. Строгое обоснование данного метода впервые было дано с помощью интегрального преобразования Лапласа. Однако использование интеграла Лапласа наталкивается на ограничения, связанные с ростом преобразуемой функции
и некоторыми функциями от этого оператора. Строгое обоснование данного метода впервые было дано с помощью интегрального преобразования Лапласа. Однако использование интеграла Лапласа наталкивается на ограничения, связанные с ростом преобразуемой функции 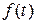 при
при  .
.
Другой путь предложен польским математиком Я. Микусиньским (1953), опиравшимся на понятие функционального кольца. Метод Микусиньского представляет собой радикальный возврат к первоначальной операторной идее. При использовании этого метода не накладывается никаких ограничений на поведении функций на бесконечности и, следовательно, область применения операционного исчисления Микусиньского значительно шире, чем операционного исчисления, основывающемся на преобразовании Лапласа.
Поскольку обе теории имеют дело с непрерывными функциями, применение операционного исчисления к решению задач имеет характер символьных преобразований. Это сужает возможности метода из-за того, что только достаточно простые задачи допускают решение в символьной форме.
При использовании численных методов непрерывные функции аппроксимируют решетчатыми функциями, которые изменяются только при целых значениях аргумента  . К решетчатым функциям можно применять дискретное преобразование Лапласа, однако по своей природе оно также более пригодно для символьных преобразований, поскольку оперирует бесконечными суммами.
. К решетчатым функциям можно применять дискретное преобразование Лапласа, однако по своей природе оно также более пригодно для символьных преобразований, поскольку оперирует бесконечными суммами.
Ниже предлагается для численного решения задач на компьютере использовать дискретную форму операционного исчисления Микусиньского, основанную на матричном представлении решетчатых функций и матричных операторах.
Решетчатую функцию обычно задают в виде бесконечной последовательности чисел:  ,
,  Если для некоторого натурального числа
Если для некоторого натурального числа 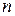 справедливо
справедливо  (
(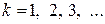 ), то тогда решетчатую функцию можно задать в виде конечной последовательности чисел:
), то тогда решетчатую функцию можно задать в виде конечной последовательности чисел:
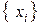 ,
,  . (11.3)
. (11.3)
В этом случае удобно пользоваться векторным представлением решетчатой функции:
 . (11.4)
. (11.4)
Обозначения (11.3) и (11.4) в дальнейшем будем считать эквивалентными друг другу. Индексы компонент вектора соответствуют аргументам решетчатой функции 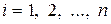 , а сами компоненты
, а сами компоненты 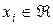 – значениям функции в соответствующих точках. Множество таких векторов размером
– значениям функции в соответствующих точках. Множество таких векторов размером 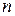 обозначим как
обозначим как  .
.
Для наших целей решетчатую функцию вида (11.3) или (11.4) удобнее представить в виде нижней треугольной матрицы размером 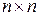
 . (11.5)
. (11.5)
Как можно видеть, первый столбец матрицы  является вектором
является вектором  . Второй получен путем единичного сдвига всех элементов первого столбца вниз. Третий – путем двойного сдвига, и т.д. Освободившиеся места замещаются нулями. Эквивалентность решетчатой функции
. Второй получен путем единичного сдвига всех элементов первого столбца вниз. Третий – путем двойного сдвига, и т.д. Освободившиеся места замещаются нулями. Эквивалентность решетчатой функции  матрице
матрице  будем обозначать следующим образом:
будем обозначать следующим образом:  .
.
Целесообразность приведенного представления объясняется тем, что для треугольных матриц сумма и произведение нижних (верхних) матриц есть также нижняя (верхняя) треугольная матрица. Обратный переход от функции-матрицы  к функции-вектору
к функции-вектору  осуществляется с помощью следующей операции
осуществляется с помощью следующей операции
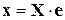 , (11.6)
, (11.6)
где 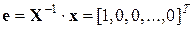 – вектор-столбец размером
– вектор-столбец размером 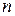 (
( ).
).
Множество нижних треугольных матриц размером 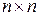 обозначается как
обозначается как 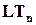 . Множество матриц вида (11.5), которое мы обозначим как
. Множество матриц вида (11.5), которое мы обозначим как 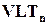 , является собственным подмножеством множества
, является собственным подмножеством множества 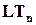 .
.
Свертка  двух решетчатых функций
двух решетчатых функций  и
и  может быть определена следующим образом:
может быть определена следующим образом:
 , (11.7)
, (11.7)
 . (11.8)
. (11.8)
Рассмотрим квадратную матрицу размером 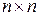 :
:  ,
,  . Если
. Если  , то
, то
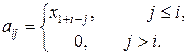 (11.9)
(11.9)
В этом случае матрица 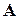 обладает свойством:
обладает свойством:
 (11.10)
(11.10)
(для любого целого 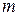 , удовлетворяющего условиям:
, удовлетворяющего условиям: 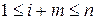 ,
, 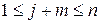 ). Если матрица
). Если матрица  обладает свойством (11.10) и
обладает свойством (11.10) и  , то очевидно, что
, то очевидно, что 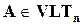 .
.
Теорема 11.1. Если  и
и 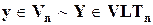 , то произведение матриц:
, то произведение матриц:  .
.
Доказательство.
1. Пусть  и
и 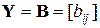 . Тогда
. Тогда 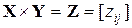 ,
,  ,
,  .
.
2. С учетом формулы (11.9): 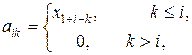

3. Отсюда следует:

4. Если 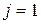 , то
, то  , что соответствует определению свертки (формула (11.8)).
, что соответствует определению свертки (формула (11.8)).
5. Если  , то:
, то: 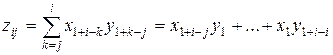 и
и 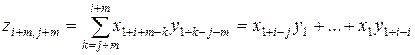 . Следовательно:
. Следовательно: 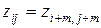 (для любого целого
(для любого целого 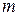 , удовлетворяющего условиям:
, удовлетворяющего условиям: 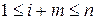 ,
, 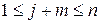 ). Поэтому:
). Поэтому:  .
.
Теорема доказана.
Следствие. Множество 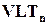 является кольцом по сложению и умножению, и умножение коммутативно (поскольку операция свертки коммутативна). Единичную матрицу будем обозначать как
является кольцом по сложению и умножению, и умножение коммутативно (поскольку операция свертки коммутативна). Единичную матрицу будем обозначать как 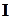 , нулевую:
, нулевую:  .
.
Рассмотрим нижнюю треугольную матрицу 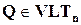 , ненулевые элементы которой, равные единице, расположены под главной диагональю:
, ненулевые элементы которой, равные единице, расположены под главной диагональю:
 . (11.11)
. (11.11)
То есть

Если эту матрицу умножить на матрицу  , то элементы произведения окажутся смещенными на одну строку вниз по сравнению с положением элементов матрицы
, то элементы произведения окажутся смещенными на одну строку вниз по сравнению с положением элементов матрицы  , а освободившиеся места замещаются нулями.
, а освободившиеся места замещаются нулями.
 .
.
Поэтому мы будем называть матрицу 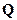 оператором сдвига. С помощью оператора сдвига можно выразить матрицу
оператором сдвига. С помощью оператора сдвига можно выразить матрицу  через компоненты вектора
через компоненты вектора 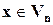 :
:
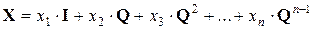 , (11.12)
, (11.12)
где 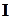 – единичная матрица.
– единичная матрица.
Если принять  , то (10.12) можно переписать в виде
, то (10.12) можно переписать в виде
 . (11.13)
. (11.13)
Теорема 11.2. Если матрица 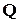 имеет размер
имеет размер 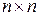 , то
, то
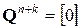 ,
, 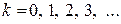 (10.14)
(10.14)