Лекция № 9. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Лекция № 9. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

 

Введение

Обыкновенные дифференциальные уравнения(ОДУ) не относятся к области дискретной математики. Мы рассмотрим этот тип уравнений для того, чтобы показать их связь с конечно-разностными уравнениями, которые изучаются в курсе дискретной математики.

Рассмотрим непрерывную функцию 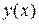, имеющую n производных: , , …, .

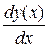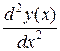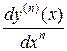Уравнение вида

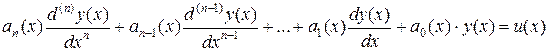, (9.1)

где 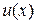и – известные функции , называется линейным ОДУ n-гопорядка.

Функция 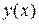заранее неизвестна. Ее получают в ходе решения дифференциального уравнения (9.1). Поэтому эту функцию называют неизвестной функцией или решением дифференциального уравнения.

В общем случае уравнение (9.1) имеет бесконечное множество решений. Чтобы выделить из них единственное решение, нужно задать начальные условия: , , …, .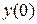

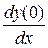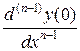Если какая-либо из производных в уравнении: 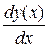, , 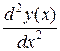…, , 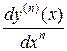либо сама функция 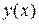, возведена в степень, отличную от первой, то такое дифференциальное уравнение называется нелинейным.

В частном случае, вместо функций , в уравнение (9.1) могут входить постоянные коэффициенты 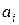(не зависящие от ). Тогда дифференциальное уравнение называется уравнением с постоянными коэффициентами.

Обыкновенные дифференциальные уравнения часто возникают при решении разнообразных физических, технических, экономических и социальных задач.

Пример 9.1.Рассмотрим электронную схему, показанную на рис. 9.1.

Рис. 9.1.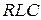-цепь

 

Схема состоит из катушки индуктивностью 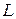, резистора сопротивлением и конденсатора емкостью . Падение напряжения на катушке определяется выражением

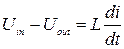, (9.2)

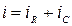, (9.3)

где – это время, 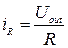– ток, протекающий через резистор, 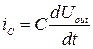– ток, протекающий через конденсатор. На основании (9.2) и (9.3) можем записать

.

После преобразований получим линейное дифференциальное уравнение второго порядка:

.

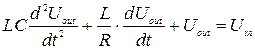В общепринятых обозначениях

. (9.4)

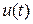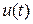Для данной электронной схемы известная функция имеет смысл входного сигнала, а неизвестная функция – это зависимый от выходной сигнал. Задавая входной сигнал и решая ОДУ (9.4), можно получать соответствующие значения выходного сигнала. Поэтому дифференциальное уравнение (9.4) является математической моделью электронной схемы, с помощью которой можно исследовать работу схемы теоретически, не собирая ее из электронных компонентов.

 

Операционное исчисление

Изобретателем операционного исчисления является Оливер Хевисайд (1859-1925), английский ученый и инженер. Он ввел оператор дифференцирования,… Пример 9.2.Применим метод Хевисайда к уравнению (9.4):

Преобразование Лапласа

. (9.5) Обратное преобразование Лапласа определяется формулой: , . (9.6)

Свойства изображений

· Всякое изображение при является аналитической функцией, то есть может быть разложено в степенной ряд и следовательно, неограниченное число раз… · Свойство линейности: если и при этом , , , то .  

Изображения некоторых функций

Непосредственным интегрированием находим . (9.7)

Основные теоремы операционного исчисления

Применяя операционное исчисление, сначала переходят от оригинала к его изображению , а затем над этим изображением выполняют операцию B,… На первый взгляд, схема решения задачи удлиняется. Однако на самом деле… Этот выигрыш достигается путем применения основных теорем операционного исчисления и известных «табличных»…

Доказательство.

  Теорема 9.7. (о свертке). Если и , то

Доказательство теоремы о свертке.

  Пример 9.5.Применяя теорему о свертке, найти оригинал изображения: .

Лекция № 10. РЕКУРРЕНТНЫЕ УРАВНЕНИЯ

 

Введение

Линейным рекуррентным уравнением с постоянными коэффициентами называется уравнение вида

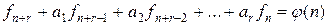. (10.1)

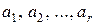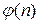Это уравнение справедливо для всех неотрицательных целых чисел n. Коэффициенты – это фиксированные числа, причём , а – заданная функция n. Если зафиксировать значения 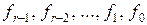и рассматривать их как начальные условия, то шаг за шагом можно однозначно определить значения 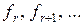, и таким образом определить всю последовательность .

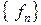Такой алгоритм удобно использовать при численном решении рекуррентного уравнения на компьютере. Однако существуют и аналитические способы решения этих уравнений. Один из таких способов использует так называемые производящие функции. Впервые метод производящих функций был применен французским математиком Лапласом (1749-1827) для решения некоторых проблем теории вероятностей.

 

Производящая функция

Пусть – производящая функция последовательности чисел , а a и b – произвольные фиксированные числа. Поскольку , то последовательности отвечает производящая функция . Это… ,

Решение однородного рекуррентного уравнения

. где – заданные числа и . Для задания начальных условий фиксируем значения . Обозначим через F(z) производящую функцию последовательности

Метод решения неоднородного рекуррентного уравнения

, n = 0, 1, 2, …, коэффициенты – это заданные постоянные, причём , а – заданная… Предположим, что одно решение уравнения найдено. Назовём это решение частным и обозначим через . Положим

Лекция № 11. ДИСКРЕТНОЕ ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ

 

Дискретное преобразование Лапласа

Функция непрерывного аргумента , определенная для всех , называется порождающей функцией для решетчатой функции .  

Основные теоремы дискретного преобразования Лапласа

2. Теорема сдвига: , . 3. Теорема смещения: .

Z-преобразование

. (11.2) В этом случае оно называется z-преобразованием. Это преобразование практически… Отыскание оригиналов по изображениям для дискретного преобразования Лапласа и z-преобразования производится по…

Дискретная интерпретация операционного исчисления Микусиньского

Другой путь предложен польским математиком Я. Микусиньским (1953), опиравшимся на понятие функционального кольца. Метод Микусиньского представляет… Поскольку обе теории имеют дело с непрерывными функциями, применение… При использовании численных методов непрерывные функции аппроксимируют решетчатыми функциями, которые изменяются…

Доказательство.

Следствие. Матрицу можно представить в виде бесконечного степенного ряда . (11.15) Замечание. Рассмотрим матрицу . Из формулы (11.15) следует

Теоремы дискретного операционного исчисления

Теорема 11.7. Если – произвольное комплексное число, то , (). (11.23)

Доказательство.

.

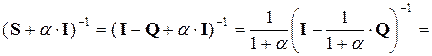
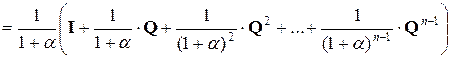Замечание. Если 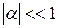, то

.

 

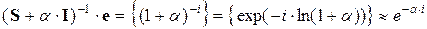Теорема 11.8.

Доказательство. Используя формулу (11.20), получим , далее , и т.д.

Теорема 11.9.

Доказательство. .  

Применение дискретного операционного исчисления

Спектр возможных приложений достаточно широк. Дискретное операционное исчисление можно использовать для численного (либо символьного) решения… где

End

>> E=I+SUM;

>> M=E*(I-Q)*inv(I+Q);

Кроме того, дискретное операционное исчисление можно использовать как численный метод решения задач непрерывной математики. Особенностью использования операционного метода для решения дифференциальных уравнений является то, что получить изображение неизвестной функции обычно не очень сложно. Трудности возникают на этапе получения оригинала этого изображения. Во многих случаях оригинал определяется только численно. И здесь может оказаться полезным дискретное операционное исчисление, в котором оператор дифференцирования 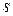приближенно заменяется матричным оператором . Это возможно в случаях, когда функция, являющаяся решением задачи, незначительно изменяется при увеличении аргумента на единицу. Можно подобрать период дискретизации решетчатой функции таким образом, чтобы это условие выполнялось. 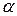Для порождающей функции , аргументом которых является произведение: , где – переменная, а – параметр, это условие эквивалентно требованию малости модуля параметра по сравнению с единицей: 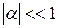. Используя разложение функции в окрестности точки в ряд Тейлора, получим:

.

Обычно 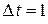. Таким образом, чем меньше по модулю параметр 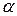, тем меньше приращение функции 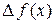. Хотя такой подход не может обеспечить абсолютно точного решения (как и любой другой численный метод), однако результат во многих случаях имеет приемлемую точность. Необходимо только при переходе от непрерывного изображения к матричному его представлению вместо единичной матрицы 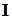использовать матрицу .

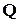Ниже дан пример решения дифференциального уравнения 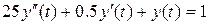при нулевых начальных условиях. Для сравнения приводится точное решение, полученное аналитическим методом.

 

Y=inv(S*(25*S^2+0.5*S+Q));

OutM=Y*Ve;

Plot(OutM), hold on

for k=1:100

Out(k)=1- exp(-0.01*k)*(cos(0.19975*k)

+0.05*sin(0.19975*k));

End

Plot(Out), hold on

Рис. 11.2  

End

>> a=1;

>> Qk=I;

>> Sum=NULL;

>> for k=1:100

Qk=Qk*Q;

a=a*abs(2*k-3)/(2*k);

Sum=Sum+a*Qk;

End

>> SRS=I-Sum;

Y=inv(SRS);

>> OutM=Y*Ve;

>> plot(OutM), hold on

>> plot(Out), hold on

 

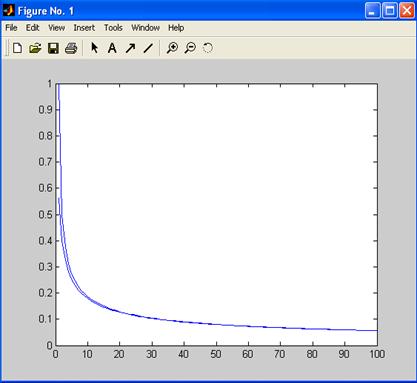
Рис. 11.3

В начале этой программы вычисляется точное значение искомой функции. Затем находится матрица и обратная ей матрица. Идентификатор SRS соответствует матрице , а идентификатор NULL – матрице с нулевыми элементами.