Доказательство.
Все элементы матрицы 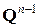 равны нулю, за исключением одного. Это элемент в нижнем левом углу, который равен единице. Поскольку матрица
равны нулю, за исключением одного. Это элемент в нижнем левом углу, который равен единице. Поскольку матрица 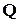 действует как оператор сдвига, то
действует как оператор сдвига, то 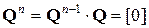 . Далее, переходя к произведению
. Далее, переходя к произведению 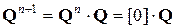 (и всем следующим за ним), учитываем, что результатом перемножения матрицы на нулевую матрицу является нулевая матрица.
(и всем следующим за ним), учитываем, что результатом перемножения матрицы на нулевую матрицу является нулевая матрица.
Следствие. Матрицу  можно представить в виде бесконечного степенного ряда
можно представить в виде бесконечного степенного ряда
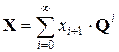 . (11.15)
. (11.15)
Замечание. Рассмотрим матрицу 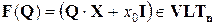 . Из формулы (11.15) следует
. Из формулы (11.15) следует
 .
.
Формально матрица  – это производящая функция последовательности чисел
– это производящая функция последовательности чисел  , аргументом которой является
, аргументом которой является 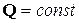 . Как сказал американский ученый Д. Гиббс: «Математика есть искусство называть разные предметы одним именем». Символы
. Как сказал американский ученый Д. Гиббс: «Математика есть искусство называть разные предметы одним именем». Символы 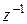 в z-преобразованиях и
в z-преобразованиях и 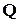 в матричных уравнениях эквивалентны друг другу, что позволяет использовать формулы z-преобразования в дискретном операционном исчислении. Однако, поскольку
в матричных уравнениях эквивалентны друг другу, что позволяет использовать формулы z-преобразования в дискретном операционном исчислении. Однако, поскольку 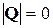 , то
, то 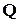 не имеет обратной матрицы.
не имеет обратной матрицы.
Теорема 11.3.
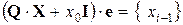 , (
, ( ). (11.16)
). (11.16)
Доказательство. Из формул (10.12) и (10.14) следует что
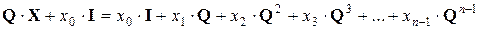 .
.
Учитывая действие матрицы 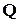 как оператора сдвига, приходим к формуле (11.16).
как оператора сдвига, приходим к формуле (11.16).
Теорема 11.4. Если 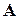 – произвольная квадратная матрица, то
– произвольная квадратная матрица, то
 . (11.17)
. (11.17)
Доказательство. Умножая обе части уравнения (11.17) справа на  , приходим к тождеству
, приходим к тождеству
 .
.
Следствие. Если  , то справедлива формула
, то справедлива формула
 . (11.18)
. (11.18)
Формула (11.18) непосредственно следует из формул (11.17) и (11.14).
Рассмотрим матрицу  , определяемую следующим образом:
, определяемую следующим образом:
 . (11.19)
. (11.19)
Теорема 11.5. Если  , то
, то
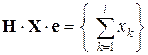 , (
, ( ). (11.20)
). (11.20)
Доказательство. На основании определения (11.12) и (11.19) можем записать:

Далее, учитывая действие матрицы 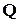 как оператора сдвига и формулу (11.6), приходим к формуле (11.20).
как оператора сдвига и формулу (11.6), приходим к формуле (11.20).
В силу свойства (11.20) матрицу  будем называть оператором суммирования. Оператор
будем называть оператором суммирования. Оператор  является дискретным аналогом оператора интегрирования
является дискретным аналогом оператора интегрирования  в операционном исчислении Микусиньского.
в операционном исчислении Микусиньского.
Оператором вычитания  назовем матрицу, определяемую выражением
назовем матрицу, определяемую выражением
 . (11.21)
. (11.21)
Теорема 11.6.
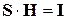 . (11.22)
. (11.22)
Доказательство. Согласно формуле (11.18):
 .
.
Оператор  является дискретным аналогом оператора дифференцирования
является дискретным аналогом оператора дифференцирования 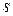 в операционном исчислении Микусиньского. Конечная разность может быть определена следующим образом:
в операционном исчислении Микусиньского. Конечная разность может быть определена следующим образом:
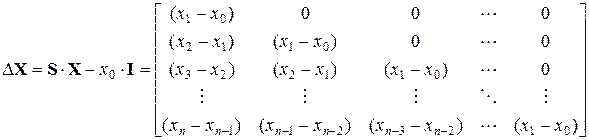 .
.