Преобразование Лапласа
Хевисайд не дал строгого математического обоснования своего метода. Это было сделано позже с помощью интегрального преобразования Лапласа. В результате такого преобразования функция 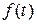 , зависящая от переменной
, зависящая от переменной  и называемая оригиналом, преобразуется в функцию
и называемая оригиналом, преобразуется в функцию  , называемую изображением (она зависит от комплексной переменной
, называемую изображением (она зависит от комплексной переменной 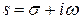 ):
):
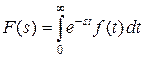 . (9.5)
. (9.5)
Обратное преобразование Лапласа определяется формулой:
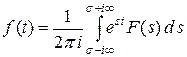 ,
, 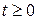 . (9.6)
. (9.6)
Чтобы интегралы (9.5) и (9.6) сходились, оригинал 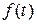 должен удовлетворять следующим условиям.
должен удовлетворять следующим условиям.
1. 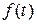 – однозначная, непрерывная или кусочно-непрерывная вместе со своими производными
– однозначная, непрерывная или кусочно-непрерывная вместе со своими производными 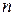 -го порядка при
-го порядка при 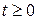 ;
;
2.  растет не быстрее, чем некоторая показательная функция, что означает существование таких постоянных положительных чисел
растет не быстрее, чем некоторая показательная функция, что означает существование таких постоянных положительных чисел 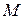 и
и  , не зависящих от
, не зависящих от  , при которых
, при которых  для всех
для всех 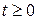 ;
;
3. 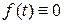 при
при  .
.
Соответствие между изображением и оригиналом обозначают следующим образом:
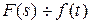 или
или  ,
,
 ,
, 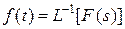 .
.
Помимо изображения по Лапласу применяется также изображение функции по Карсону (или по Хевисайду)
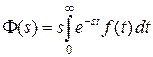 ,
,
отличающееся от преобразования Лапласа множителем 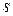 . В последнее время в технической литературе все чаще пользуются изображением по Лапласу. Это объясняется наличием наглядной связи между операторным методом и гармоническим анализом, вносящей физический смысл в понятие изображения (изображение по Лапласу
. В последнее время в технической литературе все чаще пользуются изображением по Лапласу. Это объясняется наличием наглядной связи между операторным методом и гармоническим анализом, вносящей физический смысл в понятие изображения (изображение по Лапласу 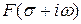 – это спектральная функция по отношению к затухающей функции
– это спектральная функция по отношению к затухающей функции 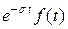 , для которой переменная
, для которой переменная  является частотой).
является частотой).