Основные теоремы операционного исчисления
В большинстве случаев применение операционного исчисления к решению задач укладывается в следующую схему. Пусть требуется найти некоторый результат в виде функции  , для получения которого без использования операторного метода надо над заданной функцией
, для получения которого без использования операторного метода надо над заданной функцией 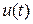 выполнить какую-то операцию A.
выполнить какую-то операцию A.
Применяя операционное исчисление, сначала переходят от оригинала 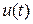 к его изображению
к его изображению  , а затем над этим изображением выполняют операцию B, соответствующую в области оригиналов операции A (например, делят изображение на
, а затем над этим изображением выполняют операцию B, соответствующую в области оригиналов операции A (например, делят изображение на 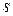 вместо интегрирования функции
вместо интегрирования функции 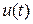 ), и получают промежуточный результат – изображение
), и получают промежуточный результат – изображение  . Затем переходят от изображения к искомому оригиналу
. Затем переходят от изображения к искомому оригиналу  .
.
На первый взгляд, схема решения задачи удлиняется. Однако на самом деле получается значительный выигрыш как в средствах вычисления, так и во времени. В частности, везде дифференцирование заменяется умножением на 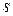 , а интегрирование – делением на
, а интегрирование – делением на 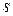 .
.
Этот выигрыш достигается путем применения основных теорем операционного исчисления и известных «табличных» изображений, публикуемых в справочниках.
Рассмотрим основные теоремы операционного исчисления.
Теорема 9.1. (о дифференцировании изображения).
Если  , то
, то  .
.
Доказательство:  .
.
Следствие 9.1.1:  .
.
Следствие 9.1.2:  . (9.20)
. (9.20)
Пример 9.3.Найти изображение функции 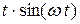 . Поскольку
. Поскольку  , то
, то 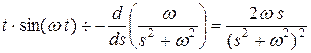 .
.
Теорема 9.2. (об интегрировании изображения).
Если  , то
, то 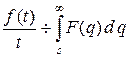 .
.
Доказательство. Обозначим  и
и 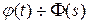 . Очевидно, что
. Очевидно, что  , и по предыдущей теореме:
, и по предыдущей теореме:
 .
.
Отсюда следует:  .
.
Постоянная интегрирования определяется из условия:  .
.

 . Таким образом
. Таким образом
 .
.
Теорема 9.3. (об изменении масштаба).
Для  всегда
всегда 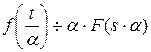 .
.
Доказательство. Обозначим 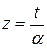 . Тогда
. Тогда
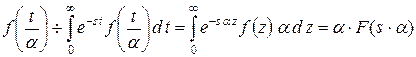 .
.
Пример 9.4.Известно, что 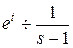 . Найти изображение функции
. Найти изображение функции 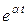 .
.
 .
.
Теорема 9.4. (запаздывания).
Если  и
и  , то
, то 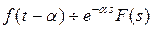 .
.
Доказательство. Обозначим  . Тогда
. Тогда
 .
.
Теорема 9.5. (упреждения).
Если  и
и  , то
, то  .
.
Доказательство. Обозначим  . Тогда
. Тогда

Теорема 9.6. (смещения).
Если  и
и  , то
, то  .
.