ВЕКТОРА НА ОСЬ.
Пусть заданы векторы 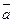 и
и 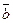 . Выберем в пространстве произвольную точку
. Выберем в пространстве произвольную точку 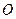 и отложим от этой точки векторы
и отложим от этой точки векторы 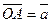 и
и  .
.
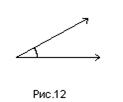
Углом между 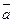 и
и 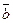 называется наименьший угол
называется наименьший угол 
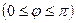 , на который нужно повернуть один из заданных векторов до его совпадения со вторым (рис.12).
, на который нужно повернуть один из заданных векторов до его совпадения со вторым (рис.12).
|
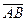 и ось
и ось  (рис.13).
(рис.13).

|
| ||||
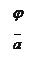 | |||||||
| | |||||||
| 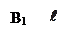 | ||||||
Обозначим через 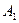 и
и 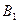 проекции на ось
проекции на ось  точек
точек 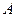 и
и  (соответственно). Построим вектор
(соответственно). Построим вектор  и назовем его компонентом вектора
и назовем его компонентом вектора 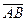 по оси
по оси  .
.
Проекцией вектора 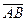 на ось
на ось  называется длина его компоненты
называется длина его компоненты  по этой оси, если компонента направлена в ту же сторону, что и ось
по этой оси, если компонента направлена в ту же сторону, что и ось  ; противоположное число, если компонента и ось имеют разные направления, нуль, если компонента есть нулевой вектор. Проекция вектора на ось обозначается в виде пр
; противоположное число, если компонента и ось имеют разные направления, нуль, если компонента есть нулевой вектор. Проекция вектора на ось обозначается в виде пр
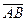 или пр
или пр =
=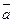 .
.
Выберем на оси  единичный вектор
единичный вектор  имеющий то же направление, что и ось
имеющий то же направление, что и ось  . Угол между векторами
. Угол между векторами 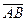 и
и  называется углом между вектором
называется углом между вектором 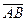 и осью
и осью  .
.
ТЕОРЕМА 13.1. Проекция вектора 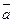 на ось
на ось  равна модулю вектора
равна модулю вектора 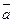 , умноженному на косинус угла
, умноженному на косинус угла  между вектором и осью:
между вектором и осью:
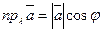 (34)
(34)
Доказательство: Пусть  и
и  является компонентой вектора
является компонентой вектора 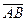 на ось
на ось  (рис.14).
(рис.14).
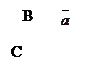 | |||||
| |||||
| |||||

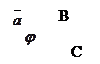 | |||||||||||
| |||||||||||
 | |||||||||||
| 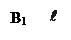 |
|
Если угол  между
между 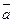 и осью острый, то компонента
и осью острый, то компонента  направлена в ту же сторону, что и ось
направлена в ту же сторону, что и ось  . Тогда
. Тогда 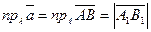 . Из треугольника
. Из треугольника 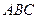 следует, что
следует, что 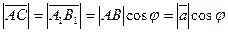 . Тогда
. Тогда 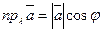 .
.
Если же 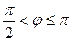 , то компонента
, то компонента  направлена в противоположную по отношению к оси
направлена в противоположную по отношению к оси  сторону. Следовательно,
сторону. Следовательно, 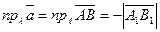 . Из треугольника
. Из треугольника 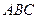 следует, что
следует, что 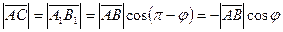 . Тогда
. Тогда  .
.
Если  , то компонента есть нулевой вектор. Тогда и
, то компонента есть нулевой вектор. Тогда и  .
.
Итак, для любых углов 
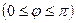
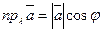 . Опираясь на ранее рассмотренные линейные операции над векторами, можно убедиться, что для проекций векторов на ось справедливы следующие теоремы (без доказательств).
. Опираясь на ранее рассмотренные линейные операции над векторами, можно убедиться, что для проекций векторов на ось справедливы следующие теоремы (без доказательств).
ТЕОРЕМА 13.2.Проекция суммы векторов на ось равна сумме проекции слагаемых векторов на ту же ось:
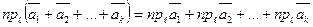 . (35)
. (35)
ТЕОРЕМА 13.3. Если вектор 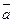 умножить на число
умножить на число  , то его проекция на ось умножится на это число:
, то его проекция на ось умножится на это число:
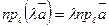 . (36)
. (36)