Окружность.
В следующих параграфах рассматриваются геометрические образы алгебраического уравнения второй степени относительно двух переменных:
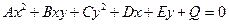 , (12)
, (12)
где 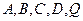 -действительные числа;
-действительные числа;
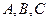 одновременно не равны нулю.
одновременно не равны нулю.
Линия, определяемая уравнением (12), называется кривой второго порядка.
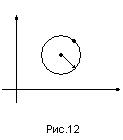
Пусть на координатной плоскости  дана окружность радиуса
дана окружность радиуса  с центром в точке
с центром в точке  и требуется определить ее уравнение (рис.12).
и требуется определить ее уравнение (рис.12).
Выберем на этой плоскости произвольную точку 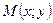 .
.
|
| |||||
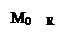 | |||||
| |||||
| |
Тогда :
1) если точка  лежит на окружности, то
лежит на окружности, то
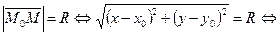
 . (13)
. (13)
2) если точка  не лежит на окружности, то для внутренних точек круга
не лежит на окружности, то для внутренних точек круга  , а для внешних точек круга
, а для внешних точек круга 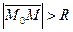 . Следовательно, для всех точек, не лежащих на окружности,
. Следовательно, для всех точек, не лежащих на окружности,
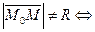
 .
.
Из 1) и 2) и определения 1.1 уравнения плоской кривой следует, что уравнение (13) есть уравнение искомой окружности.
Уравнение (13) является уравнением второй степени относительно  и
и 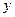 . Следовательно, окружность есть кривая второго порядка. Раскрыв скобки в уравнении (13), получим, что
. Следовательно, окружность есть кривая второго порядка. Раскрыв скобки в уравнении (13), получим, что

Сравнивая с (12), найдем, что  . Рассматривая полученные коэффициенты
. Рассматривая полученные коэффициенты 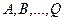 , легко заметить, что для окружности выполнились два условия:
, легко заметить, что для окружности выполнились два условия:
1) коэффициент  при произведении
при произведении 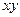 равен нулю;
равен нулю;
2) коэффициенты при 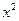 и
и  равны между собой. Покажем, что если в (12) старшие коэффициенты
равны между собой. Покажем, что если в (12) старшие коэффициенты 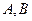 и
и 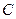 удовлетворяют условиям
удовлетворяют условиям 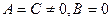 , то это уравнение определяет либо действительную окружность с
, то это уравнение определяет либо действительную окружность с 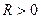 , либо точку (
, либо точку (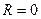 ), либо мнимую окружность (
), либо мнимую окружность (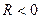 ). Полагая для простоты выкладок
). Полагая для простоты выкладок 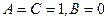 в уравнении (12), получим
в уравнении (12), получим
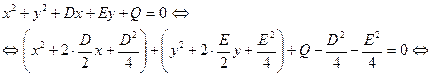
 . (14)
. (14)
Обозначим 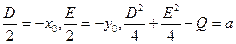 .
.
Рассмотрим три случая:
1) 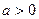 . Тогда уравнение (13) запишется в виде
. Тогда уравнение (13) запишется в виде 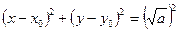 , т.е. определяет действительную окружность радиуса
, т.е. определяет действительную окружность радиуса 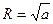 с центром в точке
с центром в точке 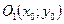 .
.
2) 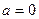 . Тогда (13) запишется в виде
. Тогда (13) запишется в виде 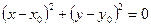 Û
Û
Û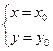 , т.е. уравнение (13) определяет единственную точку
, т.е. уравнение (13) определяет единственную точку 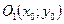 , которую можно рассматривать как «окружность» радиуса нуль;
, которую можно рассматривать как «окружность» радиуса нуль;
3) 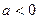 . Тогда уравнение (13) не удовлетворяется ни при каких значениях
. Тогда уравнение (13) не удовлетворяется ни при каких значениях  и
и 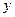 . Следовательно, уравнение (13), не определяет никакой действительно существующей кривой или для общности говорят, что оно определяет мнимую окружность с
. Следовательно, уравнение (13), не определяет никакой действительно существующей кривой или для общности говорят, что оно определяет мнимую окружность с 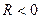 .
.
Итак, если в уравнении (12) старшие коэффициенты удовлетворяют условиям 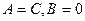 , то уравнение определяет некоторую окружность.
, то уравнение определяет некоторую окружность.
10. Эллипс.
|
 |

 |
Выберем на плоскости две произвольные точки 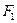 и
и  и введем систему координат
и введем систему координат  , как это показано на рис.13. Обозначим через
, как это показано на рис.13. Обозначим через 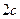 расстояние между этими точками, тогда выбранные фокусы
расстояние между этими точками, тогда выбранные фокусы 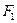 и
и  будут иметь координаты
будут иметь координаты  , а
, а 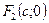 .
.
Пусть точка 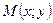 - произвольная точка плоскости
- произвольная точка плоскости  . Предположим, что точка
. Предположим, что точка  принадлежит эллипсу. Тогда, если
принадлежит эллипсу. Тогда, если 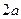 , где
, где 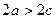 , есть сумма расстояний от точки
, есть сумма расстояний от точки  до точек
до точек 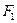 и
и  , то, по определению эллипса,
, то, по определению эллипса,
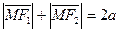 Û
Û (14)
(14)
Избавляясь от иррациональности, уравнение (14) можно привести к виду
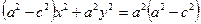 .
.
По условию 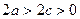 . Тогда
. Тогда 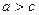 и
и 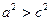 . Пусть
. Пусть 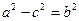 . Подставляя в уравнение (14), получим
. Подставляя в уравнение (14), получим
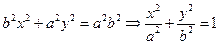 , где
, где 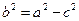 . (15)
. (15)
Пусть точка 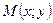 не лежит на эллипсе. Тогда для такой точки
не лежит на эллипсе. Тогда для такой точки  . Следовательно, координаты точки
. Следовательно, координаты точки  не могут удовлетворять и уравнению (15).
не могут удовлетворять и уравнению (15).
Итак, согласно определению 1.1 уравнения плоской кривой уравнение (15) есть уравнение искомого эллипса.
Уравнение эллипса (15) называется его каноническим уравнением.
Воспользовавшись уравнением эллипса, определим форму этой кривой. Так как переменные  и
и 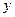 входят в (15) только в четной степени, то кривая симметрична относительно осей координат. Следовательно, достаточно определить форму кривой только в первой четверти. При
входят в (15) только в четной степени, то кривая симметрична относительно осей координат. Следовательно, достаточно определить форму кривой только в первой четверти. При 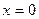 из (15) получим, что
из (15) получим, что 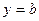 . При
. При 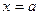 получим, что
получим, что 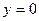 . При увеличении
. При увеличении  от 0 до
от 0 до 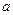 переменная
переменная 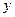 уменьшается от значения
уменьшается от значения 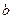 до 0. При
до 0. При 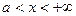
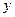 не существует. Соединяя плавной кривой точки
не существует. Соединяя плавной кривой точки 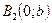 и
и 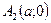 , построим искомую кривую в первой четверти (рис.13). Используя ее симметрию относительно осей координат, построим все множество точек эллипса.
, построим искомую кривую в первой четверти (рис.13). Используя ее симметрию относительно осей координат, построим все множество точек эллипса.
Терминология. Точки  и
и 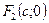 называются фокусами эллипса. Точки
называются фокусами эллипса. Точки 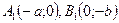 ,
,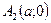 ,
,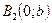 называются вершинами эллипса. Точка
называются вершинами эллипса. Точка 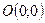 называется центром эллипса. Ось, на которой расположены фокусы эллипса, называется фокальной осью. Оси
называется центром эллипса. Ось, на которой расположены фокусы эллипса, называется фокальной осью. Оси 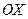 и
и 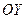 называются осями симметрии эллипса.
называются осями симметрии эллипса.
Отрезки  длины
длины 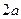 и
и  длины
длины  называются соответственно большой и малой осями эллипса. Отрезок
называются соответственно большой и малой осями эллипса. Отрезок 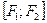 длины
длины 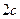 называется фокусным расстоянием.
называется фокусным расстоянием.
Отрезки  ,
, 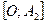 длины
длины 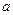 и
и 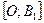 ,
, 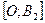 длины
длины 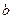 называются соответственно большой и малой полуосями эллипса. Соотношение
называются соответственно большой и малой полуосями эллипса. Соотношение  называется эксцентриситетом эллипса и обозначается буквой
называется эксцентриситетом эллипса и обозначается буквой 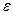 . Итак,
. Итак,
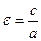 . (16)
. (16)
Так как по условию 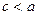 , то
, то  . Эксцентриситет характеризует форму эллипса. Действительно,
. Эксцентриситет характеризует форму эллипса. Действительно, 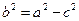 . Следовательно,
. Следовательно, 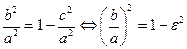 . Тогда, чем меньше
. Тогда, чем меньше 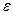 , тем меньше малая ось эллипса отличается от его большой оси. Иными словами, форма эллипса приближается к форме окружности радиуса
, тем меньше малая ось эллипса отличается от его большой оси. Иными словами, форма эллипса приближается к форме окружности радиуса 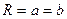 . При этом фокусы эллипса неограниченно приближаются к центру
. При этом фокусы эллипса неограниченно приближаются к центру 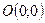 этой окружности. В пределе при
этой окружности. В пределе при 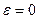 эллипс превращается в окружность.
эллипс превращается в окружность.
ПРИМЕР 9.1. Дан эллипс 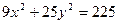 . Найти: 1) его полуоси; 2) фокусы; 3) эксцентриситет.
. Найти: 1) его полуоси; 2) фокусы; 3) эксцентриситет.
Решение. Разделив обе части уравнения эллипса на 225, найдем его каноническое уравнение 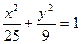 . Отсюда
. Отсюда  . Следовательно,
. Следовательно,  . Вычислим
. Вычислим 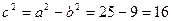 . Тогда
. Тогда 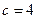 , а фокусы эллипса расположены в точках
, а фокусы эллипса расположены в точках 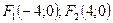 . Эксцентриситет
. Эксцентриситет 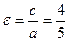 .
.