ПАРАБОЛА.
ОПРЕДЕЛЕНИЕ 11.1. Параболой называется множество всех точек плоскости, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой.
Выберем на плоскости произвольную точку 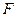 и произвольную прямую
и произвольную прямую 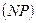 , не проходящую через эту точку. Назовем точку
, не проходящую через эту точку. Назовем точку 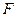 фокусом, а прямую
фокусом, а прямую 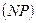 директрисой. Обозначим расстояние от точки
директрисой. Обозначим расстояние от точки 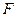 до прямой
до прямой 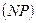 через
через 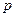 и построим систему координат
и построим систему координат  так, как это изображено на рис.16.
так, как это изображено на рис.16.

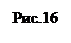
Тогда фокус будет расположен в точке 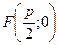 , а директриса будет иметь уравнение
, а директриса будет иметь уравнение  .
.
Пусть точка 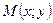 произвольная точка плоскости
произвольная точка плоскости  . Предположим, что точка
. Предположим, что точка  лежит на параболе. Тогда, по определению этой кривой
лежит на параболе. Тогда, по определению этой кривой 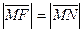 , где
, где 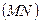 ^
^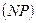 . Точка
. Точка  по построению имеет координаты
по построению имеет координаты 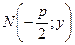 . Следовательно, равенство
. Следовательно, равенство 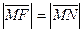 запишется в виде
запишется в виде
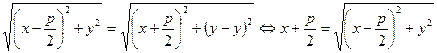 .
.
Освобождаясь от иррациональности, получим
 . (20)
. (20)
Пусть точка  не лежит на параболе. Тогда
не лежит на параболе. Тогда 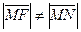 . Следовательно, и
. Следовательно, и  .
.
Итак, согласно определению 1.1 уравнения плоской кривой уравнение (20) является уравнением искомой параболы. Оно называется каноническим уравнением параболы, а число 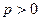 называется ее параметром.
называется ее параметром.
Определим форму параболы. В уравнение (20) переменная 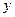 входит в четной степени. Следовательно, кривая симметрична относительно оси
входит в четной степени. Следовательно, кривая симметрична относительно оси 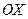 . При
. При 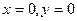 . Значит, кривая проходит через начало координат. При
. Значит, кривая проходит через начало координат. При 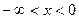 ,
, 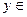 Æ, так как по условию
Æ, так как по условию 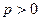 . При
. При 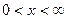
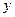 существует, причем при увеличении
существует, причем при увеличении  переменная
переменная 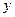 также увеличивается. По полученным данным построим параболу (рис.16).
также увеличивается. По полученным данным построим параболу (рис.16).
Терминология. Точка 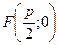 называется фокусом параболы. Точка
называется фокусом параболы. Точка 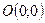 называется вершиной параболы. Прямая
называется вершиной параболы. Прямая  называется директрисой. Ось, на которой расположен фокус, называется фокальной осью. Расстояние
называется директрисой. Ось, на которой расположен фокус, называется фокальной осью. Расстояние 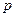 от фокуса до директрисы называется параметром параболы.
от фокуса до директрисы называется параметром параболы.
Дополнение. Если фокальную ось параболы принять за ось 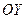 , то уравнение параболы запишется в виде
, то уравнение параболы запишется в виде
 . (21)
. (21)
ПРИМЕР 11.1. Найти фокус и уравнение директрисы параболы 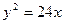 .
.
Решение. Так как каноническое уравнение параболы имеет вид  , то
, то 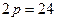 . Следовательно,
. Следовательно,  , а
, а 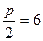 . Фокус параболы расположен в точке
. Фокус параболы расположен в точке 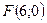 . Директриса имеет уравнение
. Директриса имеет уравнение 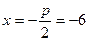 .
.