Уравнение кривых второго порядка с осями симметрии, параллельными осями координат.
Рассмотрим предварительно одну из частных задач преобразования системы координат. Пусть на плоскости введены две прямоугольные декартовы системы координат  и
и 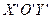 с центрами в точках
с центрами в точках 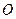 и
и  и соответственно параллельными осями координат (рис.17).
и соответственно параллельными осями координат (рис.17).

Пусть точка  в системе
в системе  имеет координаты
имеет координаты 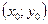 . Выберем на плоскости произвольную точку
. Выберем на плоскости произвольную точку  и обозначим ее координаты через
и обозначим ее координаты через  и
и  в соответствующих системах
в соответствующих системах  и
и 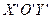 . Поставим задачу установления формул связи между координатами точки
. Поставим задачу установления формул связи между координатами точки  в старой (
в старой ( ) и новой (
) и новой (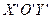 ) системах координат. Очевидно, что в системе
) системах координат. Очевидно, что в системе  вектор
вектор 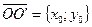 , вектор
, вектор 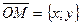 . В системе
. В системе 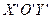 вектор
вектор 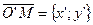 .
.
Согласно правилу сложения векторов
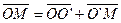 или
или  (22)
(22)
Формулы (22), связывающие между собой старые и новые координаты точки плоскости, называются формулами параллельного переноса системы координат. Пусть теперь на плоскости  задан эллипс с полуосями
задан эллипс с полуосями 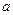 и
и 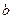 , центр которого находится в точке
, центр которого находится в точке 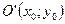 , а оси симметрии параллельны осям координат
, а оси симметрии параллельны осям координат 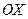 и
и 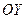 . Требуется найти уравнение эллипса. Введем новую систему координат
. Требуется найти уравнение эллипса. Введем новую систему координат 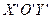 с помощью параллельного переноса системы
с помощью параллельного переноса системы  , расположив ее начало координат в центре эллипса (рис.18). Тогда в новой системе
, расположив ее начало координат в центре эллипса (рис.18). Тогда в новой системе 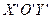 каноническое уравнение эллипса запишется в виде
каноническое уравнение эллипса запишется в виде  . Из (22) найдем, что
. Из (22) найдем, что  . Тогда в заданной системе координат
. Тогда в заданной системе координат  уравнение эллипса примет вид
уравнение эллипса примет вид

 . (23)
. (23)


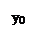

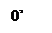



Уравнение (23) является уравнением эллипса с полуосями 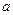 и
и 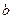 , центром в точке
, центром в точке 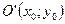 и осями симметрии, параллельными координатным осям.
и осями симметрии, параллельными координатным осям.
Решая аналогичным образом задачу относительно уравнения гиперболы с центром в точке 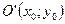 , с осями симметрии, параллельными осям координат, с действительной полуосью, равной
, с осями симметрии, параллельными осям координат, с действительной полуосью, равной 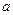 , мнимой, равной
, мнимой, равной 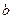 , получим уравнение
, получим уравнение
 . (24)
. (24)
Аналогично найдем, что уравнение параболы, ось симметрии которой параллельна оси абсцисс, вершина которой находится в точке 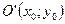 , а ее параметр равен
, а ее параметр равен 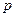 , имеет вид
, имеет вид
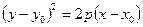 . (25)
. (25)
Если же ось параболы параллельна оси ординат, то
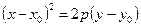 . (26)
. (26)