Исследование уравнения кривой второго порядка, не содержащего члена с произведением текущих координат.
Пусть задано общее уравнение кривой второго порядка (12) при 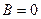 , т.е. уравнение вида
, т.е. уравнение вида
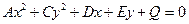 . (27)
. (27)
Покажем, что уравнение (27) в зависимости от значений коэффициентов  на плоскости
на плоскости  определяет окружность, эллипс, гиперболу, параболу, пару прямых, точку или мнимую кривую.
определяет окружность, эллипс, гиперболу, параболу, пару прямых, точку или мнимую кривую.
1. Пусть 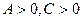 .
.
Преобразуем уравнение (27), дополнив до полного квадрата члены, содержащие переменные  и
и 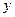 :
:
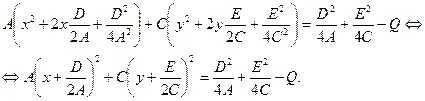
Введем обозначения, положив
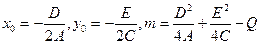 . (28)
. (28)
Тогда предыдущее уравнение запишется в форме
 . (29)
. (29)
Пусть 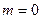 , тогда
, тогда 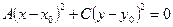 .
.
Это уравнение определяет на плоскости единственную точку 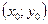 . Пусть
. Пусть 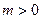 . Тогда уравнение (29) можно записать в форме
. Тогда уравнение (29) можно записать в форме
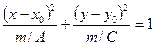 .
.
Из сравнения этого уравнения с уравнением (23) следует, что это уравнение эллипса, а значит и уравнение (27) определяет эллипс с центром в точке 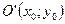 и полуосями
и полуосями 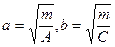 , где
, где  определяются равенствами (28).
определяются равенствами (28).
В частности, при 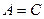 уравнение определяет окружность с центром в точке
уравнение определяет окружность с центром в точке 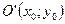 и радиусом
и радиусом 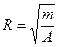 .
.
Если же в уравнении (29) 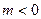 , то оно не удовлетворяется ни при каких значениях
, то оно не удовлетворяется ни при каких значениях  и
и 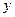 . Следовательно, уравнение (27) не определяет кривой на плоскости (или говорят: определяет мнимый эллипс). Итак, уравнение (27) при
. Следовательно, уравнение (27) не определяет кривой на плоскости (или говорят: определяет мнимый эллипс). Итак, уравнение (27) при 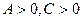 на плоскости
на плоскости  определяет либо эллипс, либо окружность, либо точку, либо мнимый эллипс.
определяет либо эллипс, либо окружность, либо точку, либо мнимый эллипс.
2. Пусть 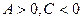 .
.
Вновь, дополняя до полного квадрата слагаемые, содержащие переменные  и
и 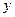 , из (27) получим
, из (27) получим
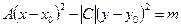 , (30)
, (30)
где  определяются равенствами (28).
определяются равенствами (28).
Если 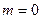 , то
, то 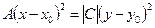
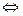
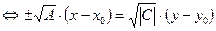 .
.
Эти уравнения определяют пару пересекающихся прямых. Если 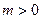 , то уравнение (30) можно записать в форме
, то уравнение (30) можно записать в форме
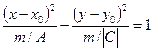 .
.
Это уравнение также определяет гиперболу с центром в той же точке 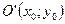 , но с действительной полуосью
, но с действительной полуосью 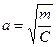 , расположенной на прямой параллельной оси
, расположенной на прямой параллельной оси 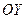 и мнимой полуосью
и мнимой полуосью 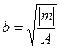 , расположенной на прямой, параллельной оси
, расположенной на прямой, параллельной оси 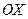 .
.
Итак, уравнение (27) при  определяет на плоскости
определяет на плоскости  либо гиперболу, либо пару пересекающихся прямых.
либо гиперболу, либо пару пересекающихся прямых.
3. Пусть 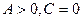 .
.
Выполняя те же преобразования, что и в предыдущих случаях, можно показать, что уравнение (27) определяет либо параболу с осью симметрии, параллельной оси 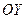 , либо пару параллельных прямых, либо мнимое место точек (доказать самостоятельно).
, либо пару параллельных прямых, либо мнимое место точек (доказать самостоятельно).
4. Если 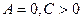 .
.
В этом случае уравнение (27) определяет либо параболу с осью симметрии, параллельной оси 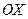 , либо пару параллельных прямых, либо мнимое место точек.
, либо пару параллельных прямых, либо мнимое место точек.
ПРИМЕР 13.1. Определите вид линии, заданной уравнением  , и изобразите эту линию на чертеже.
, и изобразите эту линию на чертеже.
Решение. Сравнивая данное уравнение с общим уравнением кривых второго порядка, найдем, что 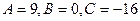 . Так как
. Так как 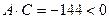 , то, согласно случаю 2, данное уравнение определяет либо гиперболу, либо пару пересекающихся прямых.
, то, согласно случаю 2, данное уравнение определяет либо гиперболу, либо пару пересекающихся прямых.
Дополняя до полного квадрата слагаемые, содержащие переменные, получим
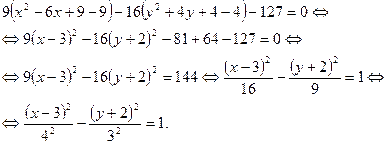
Уравнение определяет гиперболу с центром в точке 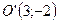 , действительной полуосью
, действительной полуосью 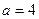 и мнимой полуосью
и мнимой полуосью  . С центром в точке
. С центром в точке  построим основной прямоугольник гипрболы со сторонами
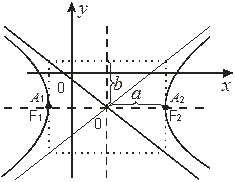
построим основной прямоугольник гипрболы со сторонами 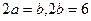 (рис.19). диагонали этого прямоугольника являются асимптотами гиперболы. Так как прямые проходят через точку
(рис.19). диагонали этого прямоугольника являются асимптотами гиперболы. Так как прямые проходят через точку 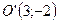 и имеют угловые коэффициенты
и имеют угловые коэффициенты 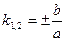 , то уравнения асимптот найдутся по формулам
, то уравнения асимптот найдутся по формулам  или
или 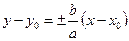 . Отсюда при
. Отсюда при 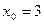 и
и 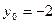 получим
получим 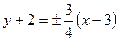 . Или
. Или 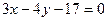 и
и 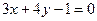 .
.
|
Вершины гиперболы при 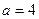 и
и  располагаются в точках
располагаются в точках 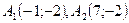 . Найдем координаты фокусов
. Найдем координаты фокусов 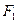 и
и 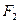 гиперболы. Вычислим
гиперболы. Вычислим 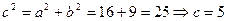 . Так как
. Так как 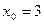 , то фокусы расположены в точках
, то фокусы расположены в точках 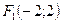 и
и 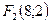 . Эксцентриситет гиперболы
. Эксцентриситет гиперболы 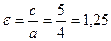 . Используя полученные результаты, построим искомую гиперболу (рис.19).
. Используя полученные результаты, построим искомую гиперболу (рис.19).
Заключение. В разделе 13 рассмотрены наиболее простые случаи расположения кривых второго порядка на координатной плоскости. В специальных курсах аналитической геометрии доказывается, что алгебраическое уравнение 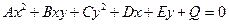 при любых старших коэффициентах
при любых старших коэффициентах 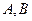 и
и 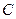 всегда определяет либо окружность, либо эллипс, гиперболу, параболу, либо вырожденную кривую (точку, прямые, мнимые кривые).
всегда определяет либо окружность, либо эллипс, гиперболу, параболу, либо вырожденную кривую (точку, прямые, мнимые кривые).