Неравенства второй степени относительно двух переменных.
ОПРЕДЕЛЕНИЕ 14.1. Неравенство 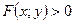 (или
(или 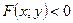 ) называется неравенством второй степени относительно двух переменных
) называется неравенством второй степени относительно двух переменных  и
и 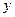 , если
, если  , где
, где  - действительные числа;
- действительные числа; 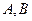 и
и 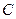 одновременно не равны нулю. Пусть дано неравенство вида
одновременно не равны нулю. Пусть дано неравенство вида
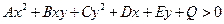 . (31)
. (31)
Выясним геометрический образ (смысл) этого неравенства на координатной плоскости  , т.е. найдем на этой плоскости множество всех точек
, т.е. найдем на этой плоскости множество всех точек 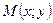 , координаты которых при их подстановке в неравенство (31) обращают его в верное числовое неравенство.
, координаты которых при их подстановке в неравенство (31) обращают его в верное числовое неравенство.
Для решения этой задачи предварительно определим вид кривой второго порядка по ее уравнению
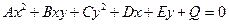 . (32)
. (32)
Допустим, что уравнение (32) определяет одну из кривых: окружность, эллипс, гиперболу или параболу. Тогда эта линия разделяет все множество точек плоскости на два или на три подмножества.
Например, окружность разделяет множество точек плоскости на множество внутренних и внешних точек круга. Выберем в любом из образовавшихся подмножеств произвольную точку 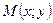 и подставим ее координаты в неравенство (31). Если при этом окажется, что (31) превращается в верное числовое неравенство, то выбранная точка
и подставим ее координаты в неравенство (31). Если при этом окажется, что (31) превращается в верное числовое неравенство, то выбранная точка  , а вместе с ней и все рассматриваемое подмножество точек плоскости, удовлетворяют заданному неравенству. Если же координаты точки
, а вместе с ней и все рассматриваемое подмножество точек плоскости, удовлетворяют заданному неравенству. Если же координаты точки  не удовлетворяют неравенству (31), то ему не удовлетворяют и все точки рассматриваемого подмножества. Применяя этот метод, называемый методом представителей, во всех случаях решения н6еравенства (32), найдем геометрический образ данного неравенства. Аналогично определяется и геометрический образ противоположного (31) неравенства.
не удовлетворяют неравенству (31), то ему не удовлетворяют и все точки рассматриваемого подмножества. Применяя этот метод, называемый методом представителей, во всех случаях решения н6еравенства (32), найдем геометрический образ данного неравенства. Аналогично определяется и геометрический образ противоположного (31) неравенства.
ПРИМЕР 14.1. Определить геометрический смысл неравенства  .
.
Решение. Определим вид кривой 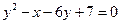 . Из сравнения с уравненим (27) получим
. Из сравнения с уравненим (27) получим 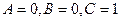 . Следовательно, кривая является либо параболой с осью симметрии, паралллельной оси
. Следовательно, кривая является либо параболой с осью симметрии, паралллельной оси 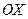 , либо парой параллельных прямых, либо мнимым местом точек.
, либо парой параллельных прямых, либо мнимым местом точек.
Дополняя слагаемые, содержащие переменную 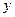 , до полного квадрата получим
, до полного квадрата получим
 . Из сравненя с уравнением параболы (25) следует, что искомой кривой является парабола с вершиной в точке (-2;3) и параметром
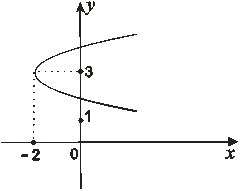
. Из сравненя с уравнением параболы (25) следует, что искомой кривой является парабола с вершиной в точке (-2;3) и параметром  .
.
|
Эта линия (рис.20) разделяет все множество точек плоскости на внутреннюю и внешнюю части I и II соответственно. Выберем произвольного представителя из люьой части. Например, выберем точку 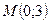 , принадлежащую внутреннему множеству точек. Подставляя ее координаты в заданное неравенство, получим 9-0-18+7=-2<0. Следовательно, точка
, принадлежащую внутреннему множеству точек. Подставляя ее координаты в заданное неравенство, получим 9-0-18+7=-2<0. Следовательно, точка  , а вместе с ней и все множество внутренних точек I не удовлетворяет данному неравенству. Тогда геометрическим образом этого неравенства будет множество внешних точек II (рис.20).
, а вместе с ней и все множество внутренних точек I не удовлетворяет данному неравенству. Тогда геометрическим образом этого неравенства будет множество внешних точек II (рис.20).
16. Поверхности и линии в пространстве  .
.
В геометрии поверхность определяется как множество точек (геометрическое место точек) пространства  ,обладающих некоторым общим для всех точек поверхности свойством. Например, сфера радиуса
,обладающих некоторым общим для всех точек поверхности свойством. Например, сфера радиуса  есть множество всех точек пространства
есть множество всех точек пространства  , удаленных на расстояние
, удаленных на расстояние  от некоторой точки
от некоторой точки 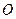 этого пространства.
этого пространства.
Рассмотрим аналитическое определение поверхности. Пусть в пространстве  введена декартова система координат
введена декартова система координат 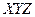 . Выберем в этом пространстве произвольную точку
. Выберем в этом пространстве произвольную точку 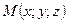 и рассмотрим вместе со множеством точек пространства
и рассмотрим вместе со множеством точек пространства  множество уравнений вида
множество уравнений вида 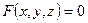 . Будем говорить, что числа
. Будем говорить, что числа  удовлетворяют уравнению
удовлетворяют уравнению 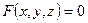 , если
, если 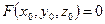 , и ему не удовлетворяют, если
, и ему не удовлетворяют, если  . Например, числа
. Например, числа 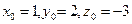 , удовлетворяют уравнению
, удовлетворяют уравнению 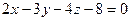 , а числа
, а числа 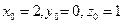
ОПРЕДЕЛЕНИЕ 15.1. Уравнение 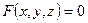 , связывающее между собой переменные величины
, связывающее между собой переменные величины 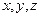 , называется уравнением поверхности в выбранной системе координат, если координаты любой (произвольной) точки
, называется уравнением поверхности в выбранной системе координат, если координаты любой (произвольной) точки  этой поверхности ему удовлетворяют, а координаты всех точек, не лежащих на ней, ему не удовлетворяют.
этой поверхности ему удовлетворяют, а координаты всех точек, не лежащих на ней, ему не удовлетворяют.
Множество всех точек координатного пространства  , координаты которых удовлетворяют уравнению, будем называть поверхностью.
, координаты которых удовлетворяют уравнению, будем называть поверхностью.
Заметим, что это множество точек может содержать бесконечное количество точек, быть конечным или быть даже пустым. Например, уравнению  удовлетворяют координаты бесконечного множества точек (сфера с центром в начале координат радиуса 1); уравнению
удовлетворяют координаты бесконечного множества точек (сфера с центром в начале координат радиуса 1); уравнению  удовлетворяют координаты только одной точки
удовлетворяют координаты только одной точки 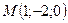 . Из определения 15.1 следует, что любое уравнение вида
. Из определения 15.1 следует, что любое уравнение вида 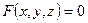 определяет в координатном пространстве некоторую поверхность.
определяет в координатном пространстве некоторую поверхность.
Как уже отмечалось, в аналитической геометрии изучаются в основном алгебраические уравнения, т.е. такие уравнения 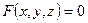 , в которых выражение
, в которых выражение 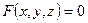 представляет собой сумму конечного числа слагаемых вида
представляет собой сумму конечного числа слагаемых вида 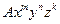 , где
, где  есть целые неотрицательные числа,
есть целые неотрицательные числа, 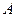 - действительное число. Наибольшая сумма
- действительное число. Наибольшая сумма 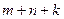 называется степенью уравнения.
называется степенью уравнения.
Например, уравнение  , где
, где  - действительные числа, есть наиболее общий вид алгебраического уравнения первой степени относительно трех переменных.
- действительные числа, есть наиболее общий вид алгебраического уравнения первой степени относительно трех переменных.
Уравнение 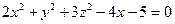 есть частный случаи алгебраического уравнения второй степени относительно трех переменных.
есть частный случаи алгебраического уравнения второй степени относительно трех переменных.
В аналитической геометрии в  линию рассматривают как множество всех точек, принадлежащих каждой из двух пересекающих поверхностей. Следовательно, система уравнений
линию рассматривают как множество всех точек, принадлежащих каждой из двух пересекающих поверхностей. Следовательно, система уравнений
 (33)
(33)
определяет уравнения линии в пространстве  .
.
Например, система  определяет окружность радиуса
определяет окружность радиуса  , расположенную на плоскости
, расположенную на плоскости  .
.