Общее уравнение плоскости.
Пусть задано произвольное алгебраическое уравнение первой степени относительно переменных 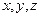
 . (36)
. (36)
Покажем, что уравнение (36) при любых допустимых значениях коэффициентов  всегда является уравнением некоторой плоскости.
всегда является уравнением некоторой плоскости.
По условию по крайней мере один из коэффициентов 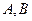 или
или 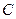 отличен от нуля. Тогда, предположив для определенности, что
отличен от нуля. Тогда, предположив для определенности, что 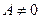 , перепишем уравнение (36) в форме
, перепишем уравнение (36) в форме
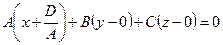 .
.
Сравнивая это уравнение с уравнением плоскости (34), найдем, что оно является уравнением плоскости, проходящей через точку 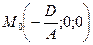 и имеющей нормальный вектор
и имеющей нормальный вектор 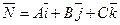 . Следовательно, уравнение (36) является уравнением некоторой плоскости при любых допустимых значениях коэффициентов
. Следовательно, уравнение (36) является уравнением некоторой плоскости при любых допустимых значениях коэффициентов  .
.
Итак, всякой плоскости в пространстве 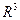 соответствует алгебраическое уравнение первой степени относительно трех переменных и всякому уравнению вида (36) соответствует плоскость. Уравнение (36) называется общим уравнением плоскости. Рассмотрим некоторые частные случаи этого уравнения:
соответствует алгебраическое уравнение первой степени относительно трех переменных и всякому уравнению вида (36) соответствует плоскость. Уравнение (36) называется общим уравнением плоскости. Рассмотрим некоторые частные случаи этого уравнения:
1) 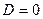 . Тогда плоскость
. Тогда плоскость 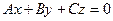 проходит через начало координат, так как точка
проходит через начало координат, так как точка 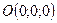 принадлежит этой плоскости при любых значениях
принадлежит этой плоскости при любых значениях 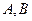 и
и 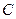 ;
;
2) 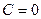 . Уравнение плоскости запишется в виде
. Уравнение плоскости запишется в виде 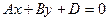 . Так как старшие коэффициенты
. Так как старшие коэффициенты 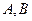 и
и 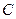 являются проекциями нормального к плоскости вектора
являются проекциями нормального к плоскости вектора  , то вектор
, то вектор 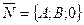 перпендикулярен этой плоскости. Но вектор
перпендикулярен этой плоскости. Но вектор  перпендикулярен и координатной оси
перпендикулярен и координатной оси 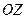 . Следовательно, рассматриваемая плоскость параллельна оси
. Следовательно, рассматриваемая плоскость параллельна оси 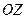 ;
;
3) если 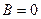 , то плоскость
, то плоскость 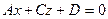 параллельна оси
параллельна оси 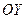 (доказать самостоятельно);
(доказать самостоятельно);
4) если 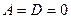 , то плоскость проходит через начало координат и параллельна оси
, то плоскость проходит через начало координат и параллельна оси 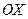 . Следовательно, плоскость
. Следовательно, плоскость 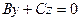 проходит через ось
проходит через ось 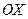 ;
;
5) если 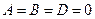 , то
, то 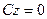 Û
Û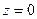 совпадает с плоскостью
совпадает с плоскостью  .
.
ПРИМЕР 18.1. Определить, перпендикулярен ли вектор 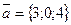 плоскости
плоскости 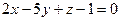 .
.
Решение. Коэффициенты 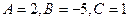 являются проекциями нормального вектора
являются проекциями нормального вектора  плоскости. Тогда, если вектор
плоскости. Тогда, если вектор 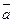 перпендикулярен заданной плоскости, то векторы
перпендикулярен заданной плоскости, то векторы  и
и 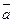 дожны быть коллинеарными. Согласно коллинеарности двух векторов проекции этих векторов должны быть иррациональными между собой. Но
дожны быть коллинеарными. Согласно коллинеарности двух векторов проекции этих векторов должны быть иррациональными между собой. Но 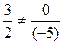 , следовательно, вектор
, следовательно, вектор 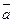 не перпендикулярен данной плоскости.
не перпендикулярен данной плоскости.