Угол между плоскостями.
Пусть в 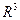 заданы своими уравнениями две плоскости
заданы своими уравнениями две плоскости
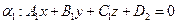 и
и 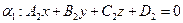 .
.
Коэффициенты 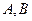 и
и 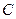 уравнения плоскости являются проекциями нормального вектора
уравнения плоскости являются проекциями нормального вектора  к этой плоскости. Следовательно, один из смежных двугранных углов
к этой плоскости. Следовательно, один из смежных двугранных углов  между плоскостями
между плоскостями  и
и  равен углу между нормальными к этим плоскостям векторами:
равен углу между нормальными к этим плоскостям векторами:
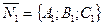 и
и 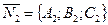 (рис.23).
(рис.23).
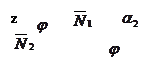 | |||
| |||

| | |||||
| |||||
|
Тогда
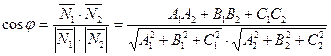 . (37)
. (37)
По формуле (37) определяется один из смежных углов между данными плоскостями.
Следствие 1. Если плоскости 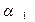 и
и  параллельны, то их нормальные векторы
параллельны, то их нормальные векторы 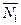 и
и 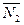 коллинеарны. Тогда
коллинеарны. Тогда
 . (38)
. (38)
Условия (38) называются условиями параллельности двух плоскостей.
Следствие 2. Если плоскости 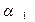 и
и  перпендикулярны, то в (37) угол
перпендикулярны, то в (37) угол 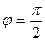 . Тогда
. Тогда 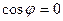 . Следовательно, и
. Следовательно, и
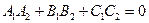 . (39)
. (39)
Условие (39) называется условием перпендикулярности двух плоскостей.
ПРИМЕР 19.1. Определить, при каком значении  плоскость
плоскость 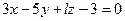 перпендикулярна плоскости
перпендикулярна плоскости 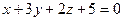 .
.
Решение. Векторы 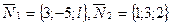 являются нормальныи векторами к данным плоскостям.тогда согласно условию (39) плоскости взаимно перпендикулярны, если
являются нормальныи векторами к данным плоскостям.тогда согласно условию (39) плоскости взаимно перпендикулярны, если 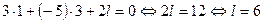 .
.
Ответ: 6.
ПРИМЕР 19.2. Составить уравнение плоскости, которая проходит через точку 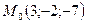 параллельно плоскости
параллельно плоскости  .
.
Решение. Искомая плоскость проходит через заданную точку 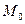 , тогда ее уравнение, согласно формуле (34), запишется в виде
, тогда ее уравнение, согласно формуле (34), запишется в виде
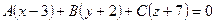 .
.
Искомая плоскость параллельна заданной плоскости. Тогда из условия параллельности двух плоскостей (38) получим
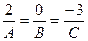 . Отсюда
. Отсюда 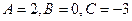 .
.
Подставляя найденные коэффициенты 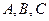 в предыдущее уравнение, найдем уравнение искомой плоскости
в предыдущее уравнение, найдем уравнение искомой плоскости
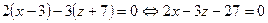 .
.
20. Прямая в пространстве 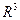 . Векторное, канонические и параметрические уравнения прямой.
. Векторное, канонические и параметрические уравнения прямой.
Положение прямой  в пространстве
в пространстве 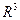 может быть определено заданием:
может быть определено заданием:
1) любых двух точек;
2) ее точки и вектора  , параллельного этой прямой;
, параллельного этой прямой;
3) 0
Поставим задачу определения уравнения прямой в каждом из этих случаев.
Пусть в пространстве 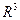 дана точка
дана точка 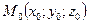 и вектор
и вектор 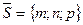 . Тогда через точку
. Тогда через точку  параллельно вектору
параллельно вектору  проходит единственная прямая
проходит единственная прямая  . Для определения ее уравнения выберем в
. Для определения ее уравнения выберем в 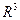 произвольную точку
произвольную точку  и построим векторы
и построим векторы
 .
.
| 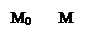 |
| |||||
 | |||
 | |||
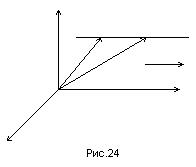
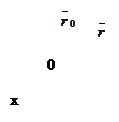
Согласно определению суммы векторов получим
 (рис.24).
(рис.24).
Пусть точка 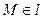 , тогда векторы
, тогда векторы 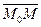 и
и  коллинеарны. Следовательно,
коллинеарны. Следовательно, 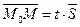 , где
, где  - параметр, принимающий любое значение из
- параметр, принимающий любое значение из  в зависимости от положения точки
в зависимости от положения точки  на прямой
на прямой  . Тогда для точки
. Тогда для точки 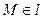 имеем
имеем
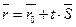 , где
, где 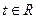 . (40)
. (40)
Если точка 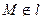 , то векторы
, то векторы 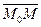 и
и  не коллинеарны.
не коллинеарны.
Следовательно, для таких точек равенство (40) не выполняется ни при каких 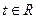 . Итак, уравнение (40) является векторным уравнением прямой, а вектор
. Итак, уравнение (40) является векторным уравнением прямой, а вектор 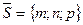 называется направляющим вектором прямой. Воспользовавшись координатами векторов
называется направляющим вектором прямой. Воспользовавшись координатами векторов 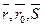 из (40), получим
из (40), получим
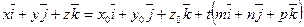 Û
Û
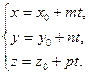 (41)
(41)
Уравнения (41) называются параметрическими уравнениями прямой  с параметром
с параметром  в пространстве
в пространстве 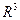 .
.
Исключая параметр  из уравнений (41), найдем, что
из уравнений (41), найдем, что
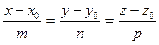 . (42)
. (42)
Уравнения (42) называются каноническими уравнениями прямой  в пространстве
в пространстве 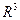 .
.
Замечание. В уравнении (42) условились считать, что числа 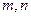 и
и 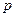 могут принимать любые значения, кроме одновременного равенства
могут принимать любые значения, кроме одновременного равенства 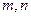 и
и 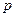 нулю. В частности, если уравнение (423) имеет вид
нулю. В частности, если уравнение (423) имеет вид 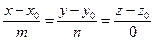 , о это уравнение есть уравнение прямой, перпендикулярной оси
, о это уравнение есть уравнение прямой, перпендикулярной оси 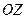 . Действительно, при
. Действительно, при 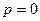 направляющий вектор
направляющий вектор 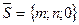 перпендикулярен оси
перпендикулярен оси 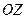 . Следовательно, и параллельная вектору
. Следовательно, и параллельная вектору  прямая перпендикулярна этой оси. Если же уравнение (42) имеет вид
прямая перпендикулярна этой оси. Если же уравнение (42) имеет вид 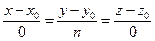 ,то это уравнение является уравнением прямой, перпендикулярной плоскости .
,то это уравнение является уравнением прямой, перпендикулярной плоскости .
ПРИМЕР 20.1. Определить, лежит ли точка  на прямой
на прямой  , проходящей через точку
, проходящей через точку 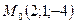 параллельно вектору
параллельно вектору 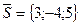 .
.
Решение. Найдем уравнения прямой  в канонической форме. Полагая
в канонической форме. Полагая 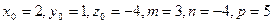 , получим
, получим 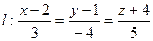 .
.
Подставляя в эти уравнения координаты точки 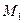 , найдем
, найдем  .
.
Следовательно, точка 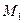 принадлежит прямой
принадлежит прямой  .
.
