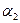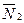Общие уравнения прямой.

 

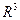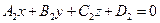Пусть в пространстве даны своими уравнениями и две плоскости . Если эти плоскости пересекаются, то система

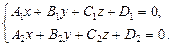(44)

определяет уравнение прямой, являющейся линией пересечения плоскостей и . Уравнения (44) называются общими уравнениями прямой.

 

Покажем, что если прямая задана своими уравнениями в одной из форм (40-44), то всегда возможно найти любую из оставшихся ее форм уравнений. Например, если прямая задана своими каноническими уравнениями 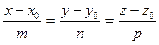, то эти уравнения равносильны системе двух уравнений первой степени

Первое уравнение этой системы не содержит . Следовательно, оно определяет плоскость, параллельную оси 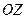. Второе уравнение не содержит и определяет плоскость, параллельную оси 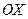. Тогда эта система составлена из уравнений пересекающихся плоскостей и представляет собой общие уравнения данной прямой .

Пусть, наоборот, прямая дана своими общими уравнениями (44) и требуется найти ее канонические уравнения. Для решения этой задачи достаточно указать одну из бесконечного множества точек 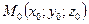, принадлежащих прямой, и найти направляющий вектор .

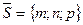Координаты такой точки проще всего определить из системы уравнений (44), если в этой системе положить либо , либо 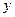, либо равными какому угодно числу (например, нулю). Для определения одного из возможных направляющих векторов пряиой построим нормальные векторы 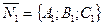, 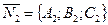данных плоскостей (рис.25).

 

 

 

 

Вектор перпендикулярен векторам , тогда

.

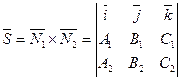Подставляя найденные координаты точки и проекции вектора в уравнения (42), найдем искомую каноническую форму уравнений заданной прямой.

ПРИМЕР 22.1. Привести общие уравнения прямой

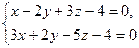к каноническом виду.

Решение. Уравнения прямой ищем в виде

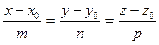(1)

Для определения координат точки в общих уравнениях положим, напрмер, 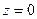. Тогда получим систему из двух уравнений с двумя неизвестными и :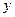

Итак, точка является одной из точе данной прямой. Для определения одного из направляющих векторов 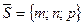прямой введем два нормальных вектора и . Тогда

.

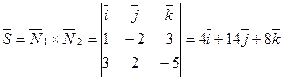Отсюда . Подставляя найденные величины в уравнение (1), получим искомую каноническую форму уравнения прямой

.
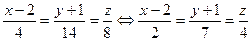