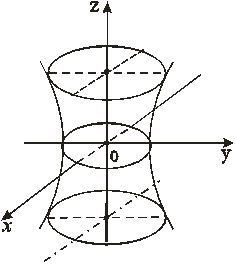
Однополостный гиперболоид.
Однополостным гиперболоидом назвается поверхность, определяемая уравнением
 (56)
(56)
В сечениях горизонтальными плоскостями 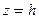 , где
, где  , получим линии
, получим линии
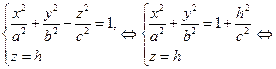
 , где
, где  .
.
Таким образом, в сечениях плоскостями 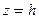 образуются эллипсы с полуосями
образуются эллипсы с полуосями 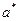 и
и 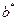 . При увеличении
. При увеличении 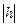 от нуля до бесконечности полуоси эллипса неограниченно увеличиваются. Наименьшие полуоси, равные
от нуля до бесконечности полуоси эллипса неограниченно увеличиваются. Наименьшие полуоси, равные 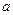 и
и 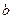 , имеет эллипс, расположенный на плоскости
, имеет эллипс, расположенный на плоскости  .
.
Пусть  , где
, где  . В сечениях образуются линии
. В сечениях образуются линии
 (1)
(1)
Если  , то
, то  . Тогда на плоскости
. Тогда на плоскости  , получим гиперболу
, получим гиперболу  , где
, где  с действительной полуосью
с действительной полуосью 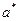 и мнимой
и мнимой  .
.
Так как действительная полуось расположена на прямой, параллельной оси 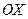 , а мнимая – параллельной оси
, а мнимая – параллельной оси 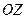 , то гипербола (1) ориентирована вдоль оси
, то гипербола (1) ориентирована вдоль оси 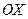 .
.
Если  , то
, то 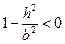 . Тогда на плоскости
. Тогда на плоскости  получим гиперболу
получим гиперболу 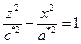 , где
, где 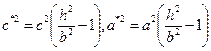 с действительной полуосью
с действительной полуосью  и мнимой
и мнимой 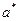 .
.
Заметим, что действительная полуось расположена на прямой, параллельной оси 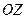 , а мнимая – параллельной оси
, а мнимая – параллельной оси 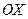 . Следовательно, гипербола (1) сменила свою ориентацию.
. Следовательно, гипербола (1) сменила свою ориентацию.
Если 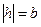 , то
, то 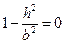 . Тогда из уравнений (1) получим
. Тогда из уравнений (1) получим
 Û
Û . (2)
. (2)
|
Уравнения (2) определяют пару пересекающихся прямых.
Итак, в сечениях вертикальными плоскостями  , где
, где  , образуются или гиперболы, изменяющий свою ориентацию, или пары пересекающихся прямых.
, образуются или гиперболы, изменяющий свою ориентацию, или пары пересекающихся прямых.
В сечениях вертикальными плоскостями 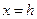 , где
, где  , образуются так же, как и в сечениях
, образуются так же, как и в сечениях  , либо гиперболы, либо пара пересекающихся прямых (исследовать самостоятельно). Полученные сечения позволяют построить искомую поверхность (рис.34).
, либо гиперболы, либо пара пересекающихся прямых (исследовать самостоятельно). Полученные сечения позволяют построить искомую поверхность (рис.34).