ОПРЕДЕЛИТЕЛИ ТРЕТЬЕГО ПОРЯДКА.
Пусть дана квадратная матрица третьего порядка
.
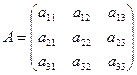ОПРЕДЕЛЕНИЕ 4.1. Определителем третьего порядка, соответствующим данной квадратной матрице А, называется число
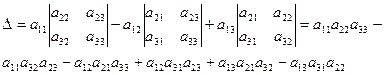(7)
Определитель третьего порядка обозначается символом
, (8)
где числа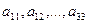 
называются его элементами.
Индексы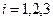 
и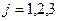 
у элемента 
показывают номера строки и столбца, на пересечении которых записан этот элемент.
Например, элемент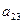 
расположен на пересечении второй строки (
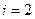) и третьего столбца (
).
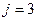Элементы 
образуют главную диагональ определителя, а элементы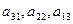 
- побочную диагональ.
Определение 4.1 имеет сложный по форме вид, поэтому для нахождения определителя третьего порядка предложены более простые правила. Так, согласно правилу треугольников необходимо:
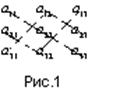
1) вычислить с собственными знаками произведения элементов, лежащих на главной диагонали и в вершинах двух равнобедренных треугольников, основания которых параллельны этой диагонали (рис.1);
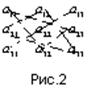
2) найти произведения элементов, лежащих на побочной диагонали и в вершинах двух равнобедренных треугольников, основания которых параллельны побочной диагонали, и взять их с противоположными знаками (рис.2);
3) найти общую сумму всех произведений.
ПРИМЕР 4.1.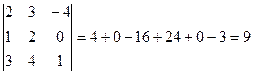 
.
Все свойства определителей второго порядка справедливы и для определителей третьего порядка. Доказательства этих свойств основаны на вычислении определителя третьего порядка по формуле (7).
Например, покажем, что определитель, у которого элементы двух его строк пропорциональны, равен нулю. Действительно,
Аналогично проверяется справедливость и других свойств.
Пусть дан определитель (8) третьего порядка.
ОПРЕДЕЛЕНИЕ 4.2. Минором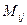 
элемента , где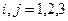 
определителя третьего порядка, называется определитель второго порядка, полученный из данного вычеркиванием 
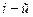строки и 
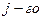столбца. Так, например, минор 
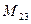элемента 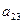есть определитель
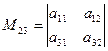, а минор элемента 
есть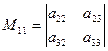 
.
С помощью миноров определитель (7) можно записать в виде
.
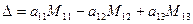ОПРЕДЕЛЕНИЕ 4.3. Алгебраическим дополнением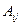 
элемента , где 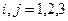, называется минор 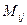этого элемента, взятый со знаком 
.
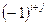Согласно определению 4.3. имеем.
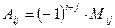, где 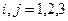. (10)
Например,
,
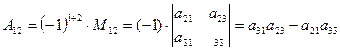и т.д.
ТЕОРЕМЕ 4.1. (Разложение определителя по элементам строки или столбца).
Определитель третьего порядка равен сумме произведений элементов любой его строки (столбца) на их алгебраические дополнения. Иными словами, имеют место шесть равенств:
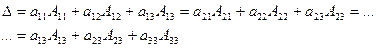(11)
Проверим, например, справедливость равенства:
.
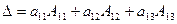Согласно определениям минора и алгебраического дополнения получим
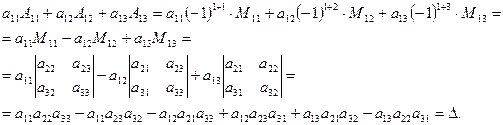
ТЕОРЕМЕ 4.2.Сумма произведений элементов какой-либо строки (столбца) определителя на алгебраические дополнения элементов любой другой его строки (столбца) равна нулю.
Для определенности выберем элементы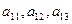 
первой строки и алгебраические дополнения 
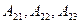элементов второй строки определителя. Составим сумму произведений 
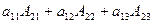и покажем, что эта сумма равна нулю.
Действительно,
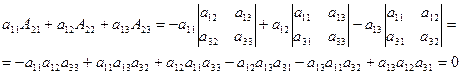
Аналогично проверяется равенство нулю и всех других подобных сумм.
В заключение рассмотрим схему использования свойств определителя и теоремы разложения при вычислении определителя.
ПРИМЕР 4.2. Вычислить определитель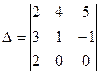 
.
Решение. Разложим определитель по элементам третьей строки.
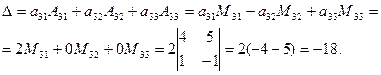
ПРИМЕР 4.3. Вычислить определитель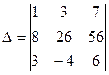 
.
Решение. Прибавляя ко второй строке первую, умноженную на -8, получим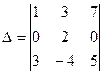 
. Раскладывая этот определитель по элементам второй его строки, найдем
.
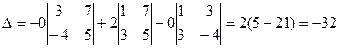ОПРЕДЕЛИТЕЛИ n-го ПОРЯДКА.
Пусть дана квадратная матрица А n-го порядка
.
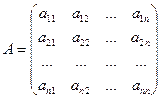Определитель n-го порядка, соответствующий квадратной матрице А, обозначается символом
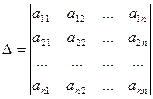(12)
и определяется как число
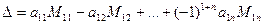, (13)
где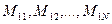 
есть миноры соответствующих элементов 
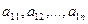, т.е. определители (n-1)-го порядка, полученные из данного вычеркиванием его первой строки и соответственно первого, второго, …, n-го его столбцов.
Например,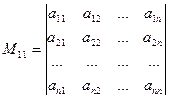 
.
Так как каждый минор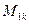 
, где k=1,2,…,n есть определитель (n-1)-го порядка, то согласно (13) вычисление определителя n-го порядка сводится к вычислению n определителей (n-1)-го порядка.
ПРИМЕР 5.1. Вычислить определитель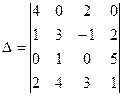 
.
Решение. Согласно (13) получим
Определители n-го порядка имеют те же свойства, что и определители третьего порядка. Их справедливость проверяется с помощью соотношения (13).
Выберем в определителе D элемент , где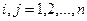 
.
Минором 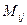элемента определителя n-го порядка называется определитель (n-1)-го порядка, полученный из D вычеркиванием его i-й строки и j-го столбца.
Алгебраическим дополнением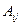элемента называется минор 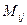этого элемента, взятый с дополнительным знаком (-1)i+j, т.е.
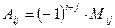, где 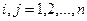. (14)
Для определителей n-го порядка также остается справедливой теореме разложения, т.е. определитель n-го порядка равен сумме произведений элементов любой его строки (столбца) на алгебраические дополнения этих элементов.
(15)
Равенство (15) содержит 2n формул, по каждой из которых можно произвести вычисление определителя.
На практике полезно перед применением теоремы разложения преобразовать определитель с помощью его свойств так, чтобы в одной из его строк (столбцов) образовалось максимальное число нулевых элементов.
ПРИМЕР 5.2. Вычислить определитель
.
Решение. Вычитая из второго столбца первый, а из четвертого столбца третий, найдем
,
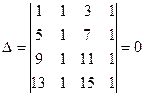так как образовавшийся определитель содержит два одинаковых столбца.