Определители. Задачи

1. Доказать свойства 2.1 и 2.5.
2. Вывести следующее правило «треугольника» для вычисления определителя матрицы третьего порядка:

.

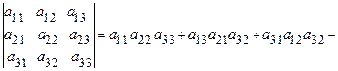
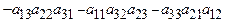1. Доказать, что
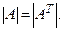
2. Квадратная матрица называется треугольной, если все ее элементы, находящиеся выше (ниже) главной диагонали, равны нулю. Доказать, что определитель треугольной матрицы равен произведению всех ее элементов на главной диагонали. В частности, .
3. Пусть даны 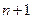функций 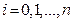. Доказать, что если все они одновременно обращаются в нуль при некотором значении 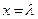, то определитель матрицы 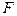, 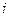-я строка которой совпадает с вектором-строкой равен нулю.
4. Квадратная матрица А называется кососимметрической, если все ее элементы на главной диагонали равны нулю, а сумма лбюых двух элементов, симметричных относительно главной диагонали, также равна нулю, т.е. . Доказать, что определитель кососимметрической матрицы нечетного порядка равен нулю.
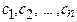5. Пусть все числа различны. Тогда матрицей Вандермонда называется матрица:

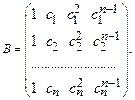
Доказать, что определитель матрицы Вандермонда равен произведению всех разностей вида 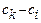, где .

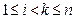1. Пусть А – квадратная матрица порядка 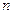. Произведение называется членом определителя, если координаты вектора 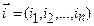составлены из номеров столбцов 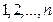(в произвольном порядке) матрицы А, а - число всех таких пар координат вектора , в которых большее число расположено в векторе раньше меньшего (такие пары называются инверсиями). Заметим, что член определителя матрицы А состоит из 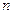сомножителей, взятых ровно по одному из каждой строки и каждого столбца матрицы.

Доказать, что сумма всех 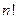членов определителя матрицы А порядк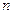а равна .