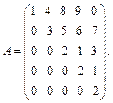Задачи для самостоятельного решения
1. Доказать следствие 4.1.
2. Доказать, что если  - собственный вектор некоторой матрицы, то и вектор
- собственный вектор некоторой матрицы, то и вектор 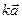 , где
, где  - любое, не равное нулю число, также является собственным вектором, соответствующим тому же собственному значению, что и
- любое, не равное нулю число, также является собственным вектором, соответствующим тому же собственному значению, что и  -
-
3. Доказать, что система векторов, состоящая из собственных векторов, соответствующих попарно различным собственным значениям некоторой матрицы А, является линейно независимой.
4. Известно следующее свойство определителя: для любых двух квадратных матриц С, В одного порядка 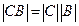 -Пользуясь этим свойством, доказать, что собственные значения обратной матрицы
-Пользуясь этим свойством, доказать, что собственные значения обратной матрицы  равны обратным величинам для собственных значений матрицы А.
равны обратным величинам для собственных значений матрицы А.
5. Доказать: нуль является собственным значением квадратной матрицы А, если и только если А – вырождена.
6. Пусть А – положительная квадратная матрица. Тогда любой ее неотрицателоьный собственный вектор является положительным и соответствует максимальному собственному значению  матрицы А.
матрицы А.
7. Пусть А – положительная квадратная матрица. Тогда любые два ее положительных собственных вектора  и
и  линейно зависимы, т.е.
линейно зависимы, т.е.  для некоторого положительного числа
для некоторого положительного числа 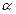 .
.
8. Для данной матрицы А найти все ее собственные значения и собственные векторы, им соответствующие.
а)  б)
б) 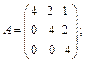 в)
в)  г)
г) 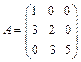 ; д)
; д)