Алгоритм Гаусса

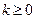-Пусть после предыдущих шагов () получена матрица 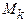. Если матрица содержит противоречивую строку, то алгоритм прекращает работу. В этом случае исходная система неразрешима. В противном случае удаляем все нулевые строки матрицы 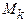, если они есть. Обозначим полученную матрицу через .

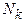- Выберем ненулевой элемент матрицы 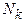и назовем его разрешающим элементом. К этому элементу предъявляется единственное требование: чтобы на предыдущих шагах он не выбирался в качестве разрешающего. Столбец и строка, содержащие разрешающий элемент, также называем разрешающими.

- С помощью элементарных преобразований все остальные элементы разрешающего столбца превращаем в нули. (Это, например, можно сделать последовательным прибавлением к строкам матрицы 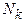разрешающей строки, умноженной на подходящее число). Таким образом, построена матрица 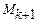.Переходим к следующему шагу.

Пример 1. Решить систему уравнений:

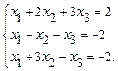
Решение. Перейдем к соответствующей матрице:

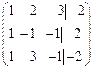В дальнейшем подчеркнутые элементы в матрицах являются разрешающими, а стрелки с числами указывают, на какое число умножается разрешающая строка и к какой строке затем прибавляется.

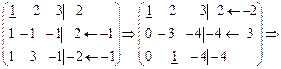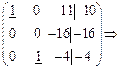
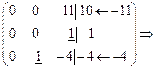
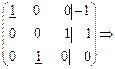
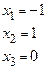
В этом примере свободных переменных не оказалось.

Пример 2. Решить систему уравнений:

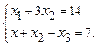
Решение. Перейдем к матрице

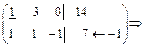
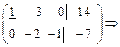
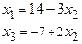
В этом примере - свободная переменная, а и - базисные переменные.

Пример 3. Решить систему уравнений:

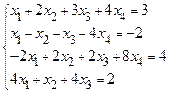
Решение. Перейдем к матрице

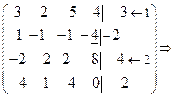
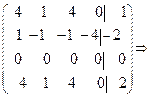
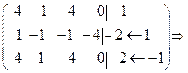
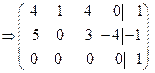Нижняя строка противоречивая, поэтому система не имеет решений.

Система (1.1) называется однородной, если все ее свободные члены 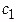, , 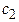…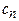равны нулю.

Однородная система линейных уравнений записывается в матричном, векторно-матричном и векторном видах:

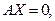
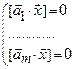, (1.2)

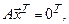
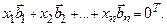(1.3)

Очевидно, что любая однородная система имеет нулевое решение. Очень важен вопрос существования ненулевого решения.

Следствие 1.1. Однородная система, в которой число уравнений меньше числа переменных имеет ненулевое решение.

Доказательство. Применим к данной системе алгоритм метода Гаусса. Так как последний столбец исходной расширенной матрицы состоит только из нулевых элементов, то в процессе элементарных преобразований он таковым и останется. Это означает невозможность появления при решении противоречивых строк. Поскольку число столбцов и, следовательно, число переменных останется неизменным, а число строк может только уменьшиться за счет вычеркивания нулевых строк, то в конечной системе число переменных будет по-прежнему больше числа уравнений. Но базисных переменных в системе столько же, сколько и уравнений. Поэтому последняя система будет обязательно содержать свободные переменные. Отсюда следует, что система имеет бесконечно много решений, в том числе и ненулевых. Следствие доказано.

Следствие 1.2. Если 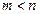, то для любой системы 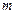векторов , , 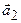…,размерности 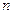существует ненулевой вектор , ортогональный с каждым вектором из этой системы.

Доказательство. От данной системы векторов , , 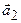…,перейдем к однородной системе (1.2), в которой число уравнений 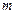будет меньше числа переменных 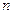. Поэтому эта система в силу следствия 1 имеет ненулевое решение , что и завершает доказательство.

Следствие 1.3. Пусть дана произвольная система векторов 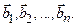Линейная зависимость этой системы векторов равносильна существованию ненулевого решения соответствующей однородной системы (1.3).

Из этого следствия вытекает, что линейную зависимость системы векторов можно проверить с помощью метода Гаусса, решив соответствующую однородную систему линейных уравнений.

Пример. Проверить линейную зависимость системы векторов:

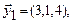
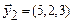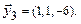
Составим соответствующую однородную систему линейных уравнений:

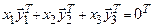расширенная матрица которой равна:

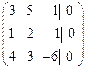Решив эту систему методом Гаусса, получим 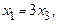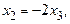что в частности означает наличие ненулевого решения. Поэтому по следствию 3 исходная система векторов линейно зависима.

Следствие 1.4. Если в системе число векторов превосходит их размерность, то система линейно зависима.

Система векторов из называется базисом пространства , если эта система линейно независимая и любой вектор из можно представить в виде линейной комбинации векторов этой системы.

Следствие 1.5. Линейно независимая система векторов из является базисом, если и только если число векторов в ней равно .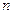

Доказательство. Предположим вначале, что линейно независимая система векторов состоит из 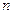векторо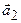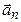в , , … , в . Добавим к этой системе произвольный вектор 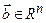. Новая система , , 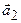… , , 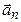будет линейно зависимой в силу следствия 4. Поэтому выполняются условия теоремы 1.4 , в силу которой вектор представим в виде линейной комбинации векторов , , 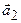… , , 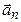т.е. , , 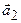… , 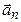- базис.

Докажем теперь обратное утверждение. Рассмотрим произвольную систему векторов , , 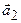…, , 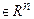где 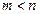. В силу следствия 2 существует ненулевой вектор , ортогональный с каждым из векторов этой системы. Если бы система векторов , , 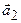…, была бы базисом, то вектор был бы представим в виде:

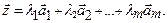
Умножим обе части этого равенства скалярно на вектор :

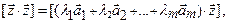
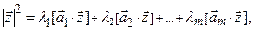
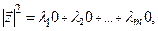
Откуда .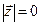

Последнее возможно только если - нулевой вектор. Полученное противоречие доказывает следствие.

Следствие 1.6. Квадратную матрицу можно привести к единичной матрице того же порядка элементарными преобразованиями строк, если и только если система строк этой матрицы линейно независима.

Доказательство. Вначале предположим, что в квадратной матрице А порядка 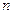система строк линейно независима. Рассмотрим однородную систему уравнений 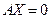и применим к ней алгоритм метода Гаусса. По аналогии с доказательством следствия 1 можно заключить, что в процессе реализации алгоритма не могут появляться противоречивые строки. Более того, не могут также появляться и нулевые строки: по теореме 1.8 элементарные преобразования сохраняют линейную независимость строк матрицы А, а наличие нулевой строки противоречило бы этому. Итак, алгоритм метода Гаусса должен привести исходную расширенную матрицу АЩ к матрице размера 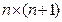с нулевым последним столбцом, в которой первые 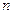столбцов будут соответствовать базису из 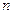переменных. Применив теперь к этой матрице элементарные преобразования типа 1, можно добиться того, что все ее ненулевые элементы станут единицами. Затем перестановкой строк, которая также осуществляется с помощью элементарных преобразований, последняя матрица приводится к едини чной, если при этом удалить последний нулевой столбец.

В случае, когда строки квадратной матрицы А линейно зависимы, по теореме 1.8 эта зависимость будет сохраняться при элементарных преобразованиях и проэтому единичная матрица получиться не может, так как ее строки линейно независимы. Следствие доказано.

Следствие 1.7.Строки квадратной матрицы линейно независимы, если и только если линейно независимы ее столбцы.

Доказательство. Рассмотри однородную систему 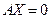. По следствию 3 линейная зависимость столбцов матрицы А равносильна существованию ненулевого решения смистемы 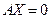. Так как система 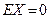имеет только нудевое решение, то по утверждению 2 наличие ненулевого решения в системе 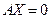равносильно невозможности с помощью элементарных преолбразований превратить матрицу А в единичную матрицу Е того же порядка, что в свою очередь равносильно линейной зависимости строк в А ввиду следствия 6.

Квадратная матрица называется невырожденной (вырожденной), если ее строки линейно независимы (зависимы)ю

Следставие 1.7 означает, что определение вырожденности матриц не изменится, если «строки» заменить «столбцами».