Методи рішення систем лінійних алгебраїчних рівнянь

У програмах аналізу в САПР для рішення СЛАР найчастіше застосовують метод Гауса або його різновиду. Метод Гауса — метод послідовного виключення невідомих із системи рівнянь. При виключенні 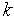-й невідомої 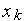із системи рівнянь

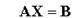
(3.16)

всі коефіцієнти при й перераховують по формулі

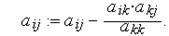
(3.17)

Виключення 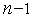невідомих, де — порядок системи (3.16), називають прямим ходом, у процесі якого матриця коефіцієнтів здобуває трикутний вид. При зворотному ході послідовно обчислюють невідомі, починаючи з .

У загальному випадку число арифметичних операцій для рішення (3.16) по Гаусу пропорційно . Це приводить до значних витрат машинного часу, оскільки СЛАР вирішується багаторазово в процесі одноваріантного аналізу, і істотно обмежує складність аналізованих об’єктів.

Можна помітно підвищити обчислювальну ефективність аналізу, якщо використати характерну практично для всіх застосувань властивість високої розрідженості матриці в моделі (3.16).

Матрицю називають розрідженою, якщо більшість її елементів дорівнює нулю. Ефективність обробки розріджених матриць велика тому, що, по-перше, перерахування по формулі (3.17) не потрібно, якщо хоча б один з елементів 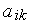або виявляються нульовим, по-друге, не потрібні витрати пам’яті для зберігання нульових елементів. Хоча алгоритми обробки розріджених матриць більш складні, але в результаті вдається одержати витрати машинного часу, близькі до лінійних, наприклад, витрати виявляються пропорційними .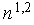

При використанні методів розріджених матриць потрібно враховувати залежність обчислювальної ефективності від того, як представлена матриця коефіцієнтів , точніше від того, у якому порядку записані її рядки й стовпці.

Для пояснення цієї залежності розглянемо два варіанти подання однієї й тієї ж СЛАР. У першому випадку система рівнянь має вигляд

 

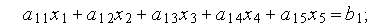
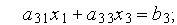
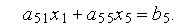
При прямому ході відповідно до формули (3.17) всі елементи матриці, які спочатку були нульовими, стають ненульовими, а матриця виявляється повністю насиченою. Елементи, що стають ненульовими в процесі гаусових виключень, називають вторинними ненулями. Вторинні ненулі в Табл. 1 відзначені знаком «*».

У другому випадку міняються місцями перше й п’яте рівняння. Матриці коефіцієнтів мають вигляд Табл. 1 і Табл. 2, де ненульові елементи представлені знаком «+». Тепер вторинні ненульові елементи не з’являються, матриця залишається розрідженою, висока обчислювальна ефективність зберігається.

Таким чином, методи розріджених матриць повинні містити в собі способи оптимального впорядкування рядків і стовпців матриць. Використовують кілька критеріїв оптимальності впорядкування. Найпростішим з них є критерій розташування рядків у порядку збільшення числа первинних ненулів, більш складні критерії враховують не тільки первинні ненулі, але й вторинні ненулі, що з’являються.